Результирующая матрица

Cтраница 2

Две результирующих матрицы 3x3 могут быть диагонализированы с целью получения двух новых наборов симметризованных волновых функций, одного - для связывающих и другого для антисвязывающих орбиталей. [16]

К результирующей матрице в случае метода полного масштабного преобразования обязательно добавляется несколько дополнительных столбцов. [17]

Для построения результирующей матрицы требуется сформировать 40 девятичленных комбинаций, то есть выписать 360 символов. [18]

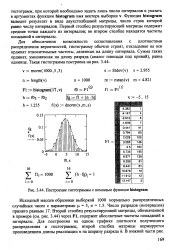Построение гистограммы с помощью функции histogram. [19]

Второй столбец результирующей матрицы, обозначенной в примере ( см. рис. 3.44) через F1, содержит абсолютные частоты попаданий в интервалы. [20]

Любой столбец результирующей матрицы является собственным вектором для Я. [21]

Докажите, что результирующая матрица передачи каскадного соединения двух отрезков линии передачи является произведением соответствующих матриц указанных отрезков. [22]

Левая верхняя клетка результирующей матрицы В имеет нужную нам форму - верхнюю почти треугольную. [23]

А-го столбца матрицы Л4 Результирующая матрица обозначается через Лй 1) и k - к основной шаг завершен. [24]

А - исходная и результирующая матрица; S - скалярная величина; М, N - целые числа, определяющие размер матрицы. [25]

Программирование разностных уравнений. [26]

Это означает, что результирующая матрица г имеет k 1 строку и пять столбцов. Каждый из столбцов содержит значения оценок соответствующей переменной модели погрешности рассматриваемой задачи. В нижней части ( см. рис 4.16) выведена структура и параметры исходных данных программного блока и график с одним из элементов вектора состояний ( погрешностью перемещений) и его оценкой. Начальная ковариационная матрица принята диагональной, что свидетельствует о принятом предположении независимости элементов начального вектора состояний. [27]

Аналогичным образом могут формироваться результирующие матрицы и для более сложных случаев, в каждом из которых следует оценивать необходимость коррекции шага интегрирования с учетом появляющегося нижнего диагонального блока результирующей матрицы А. [28]

А - исходная и результирующая матрица; S - скалярная величина; М, N - целые числа, определяющие размер матрицы. [29]

При вычитании каждый элемент результирующей матрицы представляет собой разность соответствующих элементов первоначальных матриц. [30]

Страницы: 1 2 3 4