Транспонированная матрица
Cтраница 2
Понятие транспонированной матрицы приводит к одному важному соотношению теории матриц. [16]
Значения транспонированной матрицы будут выводиться на печать построчно. [17]
Определитель транспонированной матрицы равен определителю исходное матрицы. [18]
Ранг транспонированной матрицы Ат равен рангу исходной матрицы А. [19]
Определяя транспонированную матрицу как матрицу, полученную из данной при помощи изменения роли индексов, мы можем заметить, что такие выражения, как AmiBmj, AtmBjm, AmiBjm, также сводятся к умножению строки на столбец, если предварительно выполнена подходящая перестановка индексов. [20]
Звездочками обозначены транспонированные матрицы. [21]
Штрихом обозначена транспонированная матрица. [22]
Далее строится транспонированная матрица А, которая перемножается на исходную - А А, а также на столбцовую матрицу - А В, в результате чего получается каноническая система уравнений. Эта каноническая система решается, например, методом Гаусса. Вся процедура калибровки осуществляется с помощью стандартных ЭВМ-программ. [23]
Ат - транспонированная матрица А, I - единичная матрица, a J - ( иХ) - матрица, все элементы которой единицы. [24]
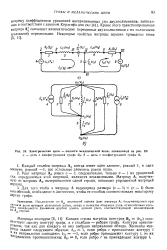 |
Электрические цепи - аналоги механической цепи, показанной на 23. [25] |
Кроме этого транспонированная матрица AJ связывает кинематические переменные двухполюсников с их полюсными ( узловыми) переменными. [26]
Хт - транспонированная матрица X - - Хг ХтХ - так называемая информационная матрица, а ( ХТХ) - 1 - матрица ошибок. Пример такого способа поиска констант дан в этом разделе, ниже. [27]
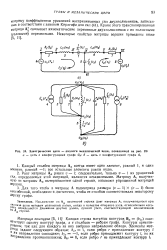 |
Электрические цепи - аналоги механической цепи, показанной на 23. [28] |
Кроме этого транспонированная матрица AJ связывает кинематические переменные двухполюсников с их полюсными ( узловыми) переменными. [29]
Мт - транспонированная матрица соединений ветвей и узлов М; ZB и YB - диагональные матрицы сопротивлений и проводимостей ветвей. [30]
Страницы: 1 2 3 4