Диагональная матрица

Cтраница 1

Диагональная матрица является частным случаем как верхней, так и нижней треугольной матрицы. Определитель треугольной матрицы равен произведению ее диагональных элементов, а именно: если T tn - треугольная матрица, то очевидно, что det Т - - п 22 tnn - Поэтому треугольная матрица является неособенной только тогда, когда все ее диагональные элементы отличны от нуля. [1]

Диагональная матрица, диагональные элементы которой равны единице, называется единичной матрицей. [2]

Диагональные матрицы р ] Cjwjb) 0 l соответствуют классическим распределениям вероятностей на множестве базисных векторов. [3]

Диагональные матрицы П и Л содержат химические сдвиги Q / и скорости поперечной релаксации X / 1 / Г2 /, а кинетическая матрица К описывает эффекты химического обмена. [4]

Диагональная матрица ( 29 7) является изображением оператора Р в своем собственном представлении. [5]

Диагональная матрица является частным случаем как верхней, так и нижней треугольной матрицы. [6]

Диагональная матрица, все элементы которой, стоящие на главной диагонали, равны между собой, называется скалярной матрицей. [7]

Диагональная матрица, у которой все элементы, стоящие на главной диагонали, равны 1, называется единичной. [8]

Диагональные матрицы, матрицы с конечными строками и матрицы с конечными столбцами образуют ассоциативные поля. [9]

Диагональная матрица diagfA, &2, &3 ] описывает линейное расширение элементарного объема в трех соответствующих направлениях. В случае k k2 k3 1 среда движется как жесткое твердое тело. [10]

Диагональная матрица слишком специальна, а симметричная матрица требует больше работы, чем наша несимметричная матрица В. [11]

Диагональная матрица ( 29 7) является изображением оператора Р в своем собственном представлении. [12]

Диагональная матрица А содержит теперь числа, обратные первоначальным числам X, и является, следовательно, обратной к первоначальной матрице А. [13]

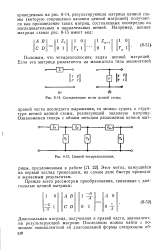Составляющие ветви цепной схемы.| Цепной четырехполюсник. [14]

Диагональная матрица, полученная в правой части, эквивалентна результирующей матрице. [15]

Страницы: 1 2 3 4