Тафелевский наклон
Cтраница 3
Таким образом, оценки ширины барьера по величине / м могут оказаться завышенными. In i / dF, соответствующее обратной величине тафелевского наклона) не зависит от температуры. Согласно любой из простых моделей Фервея или Кабрера - Мотта, эта величина, естественно, должна была бы изменяться обратно пропорционально абсолютной температуре. Девалд [159], следуя качественному рассмотрению Харинга [160], видит причину этого несоответствия в том, что граничный и пленочный барьеры имеют приблизительно одинаковую высоту, поэтому оба контролируют скорость. [31]
При переходе от одной точки поляризационной кривой к другой изменяется не только потенциал электрода, но и поверхностная концентрация реагирующего вещества. Сравнение поляризационных кривых и 6н - ср-кривых показывает, что точка изменения тафелевского наклона совпадает с началом падения заполнения поверхности углеродсодержащими частицами. [33]
Поляризационные кривые, измеренные на золотом дисковом электроде в растворе цистеина в кислой, нейтральной и щелочной средах, несмотря на одинаковый тафелевский наклон ( 0 11 В) по-разному зависят от частоты вращения диска: максимальный ток в кислой среде существенно зависит от частоты вращения электрода, а в щелочных растворах не зависит от нее - кривые, полученные на стационарном электроде и при всех изученных частотах вращения совпадают. [34]
Интегрирование предыдущего дифференциального уравнения дает упоминавшуюся выше логарифмическую зависимость. На ртути С представляет емкость только двойного слоя, которая остается примерно постоянной, при умеренных катодных потенциалах, так что dE / d Ы дает истинный тафелевский наклон Ь, а зависимость Е от Igt описывается в основном прямой линией. [35]
Тот же наклон можно получить для этого механизма, если исходить из условий Ленгмюра при заполнениях, достигших монослоя, когда они перестают зависеть от потенциала. Стандартный расчет по Ленгмюру [6, 103] в этом случае приводит к тафе-левскому наклону RT / 2F для малых заполнений и к предельному току - для больших. Таким образом, тафелевский наклон - 2RT / F ( а, принимается равным 0 5) может характеризовать промежуточную стадию реакции в значительной степени независимо от ее природы и положения в ряду последовательных стадий реакции. [36]
К тому же в принятом приближении о существовании линейной зависимости энергии от расстояния величина ( 3 постоянна, однако нелинейный участок, всегда имеющийся вблизи вершины барьера, приводит к уменьшению ( 3 с ростом ц в тех случаях, когда энергия активации мала и перенапряжение велико. Чтобы объяснить механизм электродной реакции, необходимо, во-первых, знать химические особенности реакции, число участвующих в ней электронов и состав раствора. Во-вторых, из тафелевского наклона ( см. активационное перенапряжение) следует определить коэффициент переноса а. Для простого электронного переноса он равен коэффициенту симметрии ( 3, но в более общем случае коэффициент а равен коэффициенту ( 3, умноженному на число электронов, участвующих в реакции, и зависит от других параметров суммарного процесса. Для определения порядка реакции по каждому компоненту раствора изменяют поочередно концентрацию каждого компонента и наблюдают за изменением плотности тока при постоянном потенциале. [37]
Выведенные значения тафелевского наклона остаются справедливыми также и при квазиравновесной трактовке. Хотя для стационарного состояния можно найти общие уравнения, однако при этом обычно [6, 103] выбирают соответствующие предельные значения констант скорости, что эквивалентно начальному предположению о квазиравновесии. Это следует из того, что кинетически значимые тафелевские наклоны наблюдаются в условиях, когда лимитирующей является только одна-единственная стадия, что эквивалентно-требованию об установлении квазиравновесия в предшествующих стадиях. [38]
Как будет показано ниже, тот факт, что поляризационная кривая S2Og - имеет линейный характер с наклоном b 2 303 RT / fiF ( 0 р 1), строго говоря, еще не является достаточным доказательством образования S2Og вследствие прямого разряда ионов HSO или SOJ -, хотя и служит убедительным подтверждением этого. Приведенные выше соображения можно пояснить на примере изучения анодного окисления ионов С1О - в СЮ на РЬО2 - электроде. Показано, что в данном случае такой же тафелевский наклон поляризационной кривой дает другой механизм, а че простой разряд СЮ. Для окончательного выяснения этого вопроса необходимо проанализировать всю совокупность экспериментальных фактов и сравнить их с теоретическими выводами. [39]
Реакции выделения и восстановления кислорода, несмотря на их важность, изучены меньше, чем реакция выделения водорода, поскольку их изучение представляет большие трудности. Частично это связано с тем, что многие металлы начинают анодно растворяться до того, как будет достигнут потенциал выделения кислорода. Кроме того, хотя в ряде очень тщательно выполненных работ были получены надежные тафелевские наклоны, в других работах имеются указания на изменения их со временем, что, возможно, связано с изменением поверхности электрода. Кислород сильно адсорбируется, и в результате может образоваться монослой адсорбированного кислорода или окис-ный слой в несколько молекул. Еще одним осложнением в исследовании механизма является образование ряда промежуточных, например перекисных, частиц, которые могут предположительно участвовать в реакции. [40]
Совместные исследования хемосорбции и электроокисления муравьиной кислоты на платиновом электроде показывают, что при потенциалах отрицательнее 0 35 в ( отн. Скорость электроокисления экспоненциально возрастает с ростом заполнения поверхности хемосорбированными органическими частицами. При потенциалах выше 0 35 в скорость окисления и скорость адсорбции становятся соизмеримы, что приводит к изменению тафелевского наклона поляризационной кривой, а также к снижению заполнения поверхности адсорбированными частицами. Как и в случае окисления метанола на платиновом электроде, замедленной стадией процесса окисления муравьиной кислоты является окисление органической частицы, образующейся при адсорбции и дегидрировании молекулы муравьиной кислоты, адсорбированными частицами ОН. [41]
Совместные исследования хемосорбции и электроокисления муравьиной кислоты на-платиновом электроде показывают, что при потенциалах отрицательнее 0 35 е ( отн. Скорость электроокисления экспоненциально возрастает с ростом заполнения поверхности хемосорбированными органическими частицами. При потенциалах выше 0 35 в скорость окисления и скорость адсорбции становятся соизмеримы, что приводит к изменению тафелевского наклона поляризационной кривой, а также к снижению заполнения поверхности адсорбированными частицами. Как и в случае окисления метанола па платиновом электроде, замедленной стадией процесса окисления муравьиной кислоты является окисление органической частицы, образующейся при адсорбции и дегидрировании молекулы муравьиной кислоты, адсорбированными частицами ОН. [42]
Из уравнений (10.1) и (10.2) очевидно, что оценка iKOp в зависимости от Rn требует знаний тафелевских констант Ьл и Ьс, которые могут быть неизвестны для изучаемых систем и значения которых могут меняться во время эксперимента. Определение тафелевских констант по полным т) - i-кривым для каждой изучаемой системы требует много времени и может быть не совсем точным из-за сопротивления и из-за влияния переноса вещества. Хор [90] критически отнесся к этому методу и отметил, что полное тафелевское уравнение для катодной и анодной реакций, которое определяет тафелевские наклоны, может быть использовано для расчета без использования метода измерения поляризационного сопротивления. [43]
Согласно кинетическим данным [125], окисление золота в щелочном растворе приводит к появлению области критического тока пассивации; транспассивное выделение кислорода характеризуется тафелевским наклоном 4 RT / F, что связано с наличием барьерного слоя в пленке. В кислотах наблюдается только последний наклон вплоть до наивысших исследованных плотностей тока ( 3 10 - 2 а-см-2), однако при более высоком кислородном перенапряжении эффект пассивации может наблюдаться также и в кислых растворах. Наклон кривых спада в щелочи, снятых от низких анодных потенциалов, равен 2RT / F. Было показано [125], что это значение согласуется с более низким тафелевским наклоном 4 RT / 5F, если принять, что в разрядной стадии ОН М - - МОН е возникает зависящая от потенциала равновесная псевдоемкость, а лимитирующей является следующая стадия. [44]
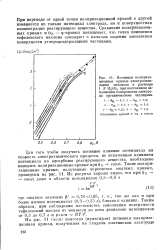
Хотя в экспериментальных условиях, представленных на рис. 1 ( а также на рис. 5), значение bi почти в два раза больше, чем &2, из этого нельзя сделать достоверного вывода, что bi имеет тенденцию достигать более низкого значения ( например, значения Ь2), когда плотность тока возрастет еще больше. Поэтому вопрос о действительном существовании стадии ( Б Г) остается открытым. Количественно другие, но в некотором отношении физически подобные результаты получают [24], если предположить, что ( Б) и ( Б Г) идут параллельно. Однако они не приведены здесь, поскольку вытекающие из этого предположения тафелевские наклоны неправдоподобны. К тому же для стадии ( Б), по-видимому, необходимо, чтобы поверхность, хотя бы умеренно, была покрыта HSO4, что кажется маловероятным. [45]
Страницы: 1 2 3 4