Вихревая напряженность

Cтраница 1

Вихревая напряженность какой-либо части жидкой поверхности остается постоянной с течением времени. [1]

Вихревая напряженность определяется так. [2]

Теория переноса вихревой напряженности Тэйлора [5] отличается от теории Прандтля тем, что пути перемешивания в выражениях для т ( и q ( t по первой теории предполагаются разными. [3]

Эта дополнительная скорость связана с вихревой напряженностью т следующим соотношением ( см. фиг. [4]

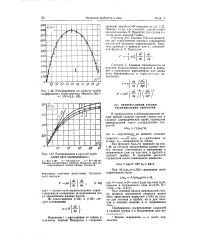Распределение по радиусу трубы коэффициента турбулентного обмена е ( Re Ы 04 - 3 2 - 106.| Распределение в круглой трубе длины пути перемешивании /. [5]

Предполагается, что при турбулентном переносе сохраняется постоянной вихревая напряженность. [6]

Аналогия между распределением тем - Р. [7]

Аналогичный характер имеет и решение уравнения (4.6) для вихревой напряженности. При небольших скоростях течения ( силы трения велики по сравнению с силами инерции) вращение частиц жидкости возникает во всей окрестности тела. [8]

Аналогия между распределением тем - Р. [9]

Уравнение (4.6) сразу переходит в уравнение (4.12), если вихревую напряженность со заменить разностью температур Ф, а кинематическую вязкость v - величиной К / рс. Граничному условию ft 0 на большом расстоянии от тела соответствует условие со О для невозмущенного параллельного течения на большом расстоянии от тела. [10]

На основании этого можно сказать, что вихревая поверхность есть поверхность, вихревая напряженность любой части которой равна нулю. [11]

Уравнение (2.110), называемое уравнением переноса вихрей, показывает, что изменение вихревой напряженности во времени и пространстве связано с диссипацией вихревой напряженности вследствие трения и характером изменения температуры в поле течения. [12]

Это уравнение, называемое уравнением переноса вихрей, показывает, что субстанциальное изменение вихревой напряженности, складывающееся из локальной и конвективной составляющих, равно диссипации вихревой напряженности вследствие трения. К уравнению (4.6) необходимо, конечног присоединить уравнение неразрывности ( 4.4 а), следовательно, для определения двух составляющих и, v скорости мы имеем два уравнения. [13]

Потенциальное течение вызывается стоком с расходом Q в вершине конуса и потенциальным вихрем с вихревой напряженностью Г вокруг оси конуса. [14]

Действительно, если жидкая поверхность S есть вихревая поверхность в определенный момент 0, то вихревая напряженность каждой части поверхности равна нулю. [15]

Страницы: 1 2