Установившееся автоколебание

Cтраница 3

Здесь следует указать, что не всякий режим с постоянными амплитудами колебаний является нейтральным и соответствует границе устойчивости. Тем же свойством обладает и режим установившихся автоколебаний, хотя он соответствует области неустойчивости. Однако в отличие от нейтральных колебаний автоколебания описываются нелинейными системами уравнений и сам факт анализа нелинейной системы в дальнейшем изложении будет особо оговариваться. [31]

Фазовая диаграмма в случае быстрого движения ленты ( или малого коэффициента трения. [32]

С этого момента снова начинается проскальзывание, и фазовая траектория дальнейшего движения бруска представляет собой окружность с центром в точке хй. Это и есть значение амплитуды А установившихся автоколебаний. [33]

Под установившимся процессом в этом случае понимается обычно процесс поддержания экстремума какого-либо показателя качества. Объектами рассмотрения и расчета в установившемся процессе могут быть амплитуда и частота установившихся автоколебаний около значения экстремума, а также устойчивость предельного цикла. Постановка задачи в этом случае сама говорит о целесообразности применения для исследования искомого Процесса того или иного математического аппарата. [34]

Замкнутую АСР с П - регулятором ( или ПИ-регулятором, превращенным в П - регуля-тор за счет установки бесконечно большого значения Тиз) путем постепенного увеличения / Ср выводят на границу устойчивости. Для этого режима определяют / ср хр и Таер кр - период установившихся автоколебаний, по которым и рассчитывают оптимальные параметры настройки регулятора. [35]

Следует иметь в виду, что современное состояние теории таково, что задачи вибрационного горения, как и явления Рийке, решаются в линейном приближении - основные исходные уравнения гидродинамики и уравнения, описывающие свойства теплоподвода, линеаризуются. Как известно, линейная теория не может дать ответа на вопрос о величине амплитуды установившихся автоколебаний; это может сделать лишь теория, учитывающая нелинейность процессов. Отсюда видно, насколько важно построение теории с учетом нелинейностей. Однако, в силу математических трудностей, учет нелинейностей в задаче об автоколебаниях тепловых систем фактически еще не проводился достаточно корректно. Таким образом, хотя в задачах, связанных с вибрационным горением, нелинейности определяют характер процесса, теория этих явлений по существу линейна. В данной книге мы не только излагаем теорию нелинейных акустических явлений, но и делаем попытку подвести читателя к постановке тех задач, которые должны решаться с учетом нелинейностей. [36]

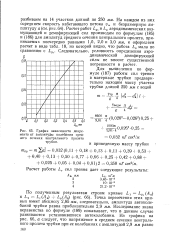График зависимости декремента от амплитуды колебания среднего сечения центрального пролета трубки. [37]

Точка пересечения этих кривых имеет абсциссу 2 85 мм, следовательно, амплитуда автоколебаний трубки равна приблизительно 2 9 мм. Исследование знака неравенства по формуле ( 189) показывает, что в данном случае развиваются установившиеся автоколебания. [38]

Выше, рассматривая усилитель, охваченный обратными связями ( § 1 - 1), было показано, что установившиеся автоколебания будут существовать при условии, что Ку 1 - Если же Ку 1, то амплитуда колебаний будет непрерывно расти. [39]

В этом случае расходящиеся от точки М фазовые траектории приходят в устойчивые узлы, не показанные на рисунке. В этом случае расходящиеся от точки М спирали фазовых траекторий все свиваются к замкнутой кривой, называемой предельным циклом ( рис. 22.34), который и соответствует установившимся автоколебаниям. Если, согласно начальным условиям, начальная точка окажется вне предельного цикла, то фазовая траектория, свиваясь, приходит также к этому предельному циклу. [40]

В зтом случае расходящиеся от точки М фазовые траектории приходят в устойчивые узлы, не показанные на рисунке. В этом случае расходящиеся от точки М спирали фазовых траекторий все свиваются к замкнутой кривой, называемой предельным циклом ( рис. 4 - 32), который и соответствует установившимся автоколебаниям. Если, согласно начальным условиям, начальная точка окажется вне предельного цикла, то фазовая траектория, свиваясь, приходит также к этому предельному циклу. [41]

Цикл 1 неустойчивый, а цикл 2 устойчивый. Этот случай отличается от рис. 8 - 11, а тем, что при больших отклонениях от установившегося режима возникают колебания, которые не расходятся бесконечно, а стягиваются к установившимся автоколебаниям. [42]

Необходимое для возникновения автоколебаний периодическое воздействие обусловлено механизмом возбуждения, имеющимся непосредственно в самой системе станок - деталь - инструмент и преобразующим постоянное по времени воздействие от источника энергии - электродвигателя в переменное; при этом частота и амплитуда возникающих в процессе резания установившихся автоколебаний определяется только параметрами системы. В реальной упругой системе в процессе резания может быть значительное число физических явлений, создающих механизм возбуждения, обусловленных: 1) свойствами упругой системы; 2) процессом резания и 3) взаимодействием факторов, определяющих свойства упругой системы с несколькими степенями свободы и особенностями протекания процесса резания. [43]

Наиболее интересным обстоятельством следует признать то, что вне зависимости от величины угла Ф в тех случаях, когда происходит самовозбуждение, амплитуду колебаний можно считать практически неизменной. При этом величина амплитуды колебания скорости несколько превышает среднюю скорость течения i050 м / сек. Следовательно, при установившихся автоколебаниях должен наблюдаться периодический заброс пламени в область перед стабилизатором. [44]

Другая важная особенность автоколебаний состоит в том, что их амплитуда полностью определяется свойствами системы и не зависит от начальных условий, тогда как амплитуда свободных колебаний консервативной системы существенно зависит от начальных условий. Таким образом, особенностью предельного цикла является его полная независимость от начальных условий; после любого возмущения состояния равновесия система приближается к одному и тому же предельному циклу. Для выявления параметров ( частоты, амплитуды) установившихся автоколебаний необходим анализ соответствующей нелинейной задачи. [45]

Страницы: 1 2 3 4