Хаотическое автоколебание
Cтраница 1
Возникновение хаотических автоколебаний в генераторе на основе двухрезонаторного пролетного клистрона, охваченного внешней обратной связью подробно рассматривалось в лекции 2 первого тома, где приводились соответствующие численные и экспериментальные данные. [1]
Описанная выше фазовая синхронизация хаотических автоколебаний наблюдается при средних амплитудах внешней силы. [3]
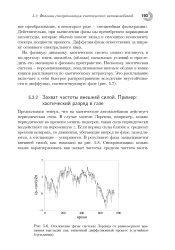 |
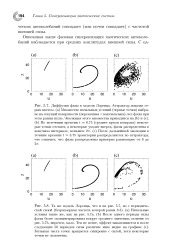
Отклонение фазы системы Лоренца от равномерного вращения выглядит как типичный диффузионный процесс ( случайные блуждания. [4] |
Предположим теперь, что на хаотические автоколебания действует периодическая сила. Если период силы близок к среднему времени возврата, то движения, убегающие вперед по фазе, замедляются, а отстающие - ускоряются. [5]
Представляется уместным описать фазовую синхронизацию хаотических автоколебаний в общем контексте явления захвата частоты. На рис. 5.9 сравниваются периодические, шумовые и хаотические колебания. Захват фазы периодических автоколебаний - полный, он может быть реализован при сколь угодно малой амплитуде силы. Для захвата фазы шумовых и хаотических колебаний необходимо подавить диффузию фазы, поэтому в этих случаях обычно имеется порог синхронизации по амплитуде силы. Отметим также, что захваченные колебания остаются шумовыми или хаотическими: сила вносит в движение некоторый порядок ( идеальный ритм), но не делает его полностью регулярным. [7]
Понятно, что такая концепция синхронизации хаотических автоколебаний не исчерпывает всего спектра наблюдаемых явлений при воздействии сигнала сложной формы на генератор хаотических колебаний. [8]
Сплошной спектр характерен для всех систем, совершающих хаотические автоколебания, тогда как дискретным спектром обладают системы с регулярным ( периодическим или квазипериодическим) временным поведением. Таким образом, изучение спектра автокорреляционной функции, так же как и расчет энтропии Колмогорове позволяет отличать временной порядок от хаоса. [9]
Актуальной является и задача о влиянии внешнего сигнала на хаотические автоколебания в системах релятивистской вакуумной электроники. Влияние внешнего сигнала позволяет в этом случае либо упростить спектральный состав выходного излучения, поднять КПД и выходную мощность, либо, наоборот, получить близкий к шумовому спектр выходного сигнала, и опять же поднять КПД и выходную мощность, но уже в режиме генерации хаотического сигнала. [10]
Излагается новый бурно развивающийся раздел теории нелинейных колебаний - стохастические и хаотические автоколебания в динамических системах. Исследование этих проблем весьма актуально для многих областей науки, позволяет по-новому взглянуть на известные явления, например турбулентность в жидкости, газе и плазме, предсказывать возможность сложного поведения конкретных систем разной природы. Книга иллюстрирована множеством примеров механических, физических, химических и биологических систем, в которых наблюдаются стохастические и хаотические колебания. [11]
Излагается новый бурно развивающийся раздел теории нелинейных ьо-лебаний - стохастические и хаотические автоколебания в динамических системах. Исследование этих проблем весьма актуально для многих областей пауки, позволяет по-новому взглянуть на известные явления, например турбулентность в жидкости, газе и плазме, предсказывать возможность сложного поведения конкретных систем разной природы. В книге приведено множество примеров механических, физических, химических и биологических систем, в которых наблюдаются стохастические и хаотические колебания. [12]
Кроме реализации в виркаторе-клистроне генерации, близкой к од-ночастотной, в нем возможны режимы хаотических автоколебаний с широким спектром генерации. [13]
Так же как и в случае периодических колебаний, важно различать автоколебания и вынужденные движения. Хаотические автоколебания описываются автономными уравнениями, поэтому все моменты времени эквивалентны. Есть много примеров хаотических движений в нелинейных системах с периодической внешней силой, они описываются неавтономными уравнениями. [14]
Для этого достаточно взять большой интервал времени г и сосчитать число максимумов N ( r) переменной z на этом интервале ( или сосчитать число других событий, выбранных для построения отображения Пуанкаре); отношение r / 7V ( r) даст средний период. Основная идея фазовой синхронизации хаотических автоколебаний состоит в возможности захвата этой частоты периодической внешней силой или же в возможности ее подстройки к частоте другого хаотического осциллятора в результате их взаимодействия. Для более детального описания процесса полезно определить фазу хаотических автоколебаний. [15]
Страницы: 1 2