Несовместность

Cтраница 3

В заключение необходимо заметить, что несовместность системы ограничений во всех случаях устанавливается на начальной стадии решения задачи - при нахождении опорного плана. [31]

Соотношение (2.4) позволяет по известному тензору несовместности находить распределение упругих деформаций. [32]

Найдем отличные от нуля компоненты тензора несовместности и их связь с прогибом границы. [33]

Поскольку TMS доверяет решателю задач указывать на несовместность, помечая вершину как противоречивую, решателю задач также доверяется и использование немонотонных предположений для любого допущения, к которому можно применить обратное прослеживание. Поскольку TMS не проверяет те утверждения, которые представляют вершины, она отказывается, например, от возможности удаления подтверждений типа посылок. [34]

И здесь возможны случаи неограниченности многогранника или несовместности системы. [35]

Таким образом, вывод о совместности или несовместности системы уравнений следует сразу из системы уравнений после преобразования по Гауссу. [36]

Через конечное число шагов мы либо обнаружим несовместность системы ограничений, либо включим все уравнения (4.2) в число базисных. Подтверждения требует лишь неособенность матрицы, соответствующей этой паре, что легко следует из способа набора базисных ограничений и уравнений: очередное значение базисной неизвестной определялось из очередного базисного ограничения через ранее уже найденные базисные неизвестные. Это означает треугольность и неособенность базисной матрицы. [37]

Как правило, решение задачи оперативно-календарного планирования при несовместности системы ограничений связано с коррекцией текущих планов. Нетрудно показать, что при этом исходную систему ограничений всегда можно сделать совместной. Действительно, решение исходной задачи xwt - 0 при любых компонентах векторов v wt и & kt удовлетворяет всем ограничениям задачи, кроме плановых ограничений ( VIII. Следовательно, при обнаружении несовместности системы ограничений необходимо, во-первых, определить, какой именно из текущих планов производства подлежит коррекции, во-вторых, на сколько именно его следует снизить. Обычно при несовместной системе ограничений величину коррекции текущего плана не определяют; задачу решают без плановых ограничений ( VIII. Выбор же текущего плана, подлежащего коррекции, остается за персоналом предприятия. [38]

В I случае задача не имеет решения из-за несовместности системы ограничений в области допустимых решений; во II случае задача всегда имеет оптимальное решение; в III случае, в зависимости от направления вектора С ( от коэффициентов функции г), задача может иметь или не иметь решения. Последнее связано с неограниченным возрастанием ( zmax - -) или убыванием ( 2rain - оо) функции г в области допустимых решений. [39]

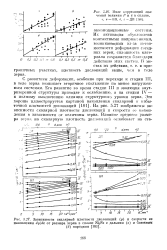Поле корреляций значений величин Р и Ч в сплаве.| Зависимости скалярной плотности дислокаций ( р п скорости ее накопления dp / de от размера зерна в сплаве Ni3Fe с дальним ( а и ближним. [40]

Их активация обусловлена контактными напряжениями, возникающими из-за несовместности деформации соседних зерен, сплошность материала сохраняется благодаря действию этих систем. [41]

Есть ли основания опасаться потери точности решения системы из-за несовместности, появившейся в результате влияния ошибок округления. [42]

Отметим что при доказательстве еущеетвшнв - использовалось яредяоложе-ние о несовместности событий. [43]

Является ли взаимная противоположность событий необходимым и достаточным условием их несовместности. [44]

Есть ли основания опасаться потери точности нормального псевдорешения системы из-за несовместности, появившейся в результате влияния ошибок округления. [45]

Страницы: 1 2 3 4