Неточность - уравнение
Cтраница 2
Линейная зависимость сохраняется в ряде случаев до давлений в несколько атмосфер. При высоких температурах неточность уравнения ( IV, 67) возрастает в связи с резким уменьшением величин Я2 и AI и возрастанием отклонения пара от идеальных законов. [16]
Линейная зависимость сохраняется в ряде случаев до давлений в несколько атмосфер. При высоких температурах неточность уравнения ( IV, 67) возрастает в связи с резким уменьшением величин Ая и AI и возрастанием отклонения пара от идеальных законов. [17]
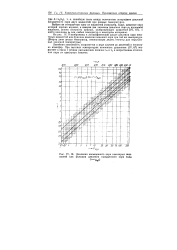 |
Давления насыщенного пара некоторых жидкостей как функции давления насыщенного пара воды. [18] |
Линейная зависимость сохраняется в ряде случаев до давлений в несколько атмосфер. При высоких температурах неточность уравнения ( IV, 67) возрастает в связи с резким уменьшением величин Ха и Xj и возрастанием отклонения пара от идеальных законов. [19]
Оценивая точность ( VII, 38), следует иметь в виду, что отклонение от него становится значительным даже при не очень высоких давлениях. Это объясняется не столько неточностью уравнения Менделеева - Клапейрона, сколько наложением на рассматриваемый эффект другого эффекта, также количественно изменяющегося с давлением, - растворения жидкости в сжатом газе ( см. гл. [20]
При помощи описываемого метода были вычислены приближенные значения А7 / т в интервале 298 - 1000 К для 20 углеводородов шести гомологических рядов ( табл. 47), для которых экспериментальные данные в литературе отсутствуют. Хотя в уравнении ( IX44) аккумулированы неточности уравнений ( IX36), ( 1Х 37) и ( 1Х 41), однако можно полагать, что Дср для этих веществ не будет превышать 0 3 ккал / молъ. Если не ставить перед собой задачу получения очень точных результатов, то указанное число веществ можно было бы значительно увеличить, а также определить для многих углеводородов зависимость АЯг от Т при низких температурах, при которых данные особенно скудны. [21]
Безразмерное отношение (59.7) называется критическим коэффициентом. Указанное расхождение с опытом лишний раз свидетельствует о неточности уравнения Ван-дер - Ваальса. [22]
Еще сравнительно недавно в одной из работ [23] утверждалось следующее: Вопреки существующему иногда мнению, вывод или запись уравнений системы более важны, чем исследование самих уравнений. Действительно, практика показывает, что большинство ошибок возникает в результате неточности уравнений, а не из-за ошибочных решений. Кроме того, уже полученные уравнения могут быть решены и изучены при помощи вычислительной машины, однако ни одна вычислительная машина не в состоянии записать уравнения системы. [23]
 |
Схема образования алмаза из графита ( а и зависимость изменения толщины межфазной области от размера кристалла алмаза ( 6. [24] |
Результаты измерений подтверждают найденный теоретически линейный характер зависимости 6 от га. Отклонение экспериментальных данных от расчетных могут быть объяснены, во-первых, неточностью экстраполяционного уравнения ( 54), во-вторых, выражение ( 53) предполагает, что растущий кристалл со всех сторон окружен графитом, а высвободившаяся межфазная область полностью заполняется расплавленным металлом. [25]
Кроме достоинств, связанных с простотой расчета более сложных задач, этот метод по сравнению с ньютоновским имеет принципиальное преимущество с логической точки зрения. Ведь на самом деле уменьшение точности конечных результатов объясняется вовсе не одной только неточностью уравнений и неточностью определения начальных условий; вообще все имеющиеся у нас данные содержат принципиальную неточность. Поэтому бессмысленно сначала получать результат с искусственно повышенной точностью, а затем специально изучать ошибки при расчете, с тем чтобы выяснить его реальную точность. Мы можем с самого начала выложить все наши карты на стол; в конце концов при этом мы получим ровно то, что нам нужно, не больше и не меньше. Такой подход не только позволяет сэкономить много ненужных усилий, но и приводит к повышению реальной точности расчетов. [26]
Очевидно, что замена свободной поверхности преградой с малой динамической жесткостью приводит к увеличению расстояния между плоскостью откола и контрольной поверхностью, где проводятся измерения. В результате возможные искажения волнового профиля также возрастают. Кроме того, применение преград сопряжено с появлением дополнительных источников погрешности, обуславливаемых неточностью уравнений состояния образца и преграды и необходимостью определения малой разности больших величин. Погрешность уменьшается с увеличением разности динамических импедан-сов образца и преграды. [27]
Формула показывает, что отравляющее действие меди в 70 раз сильнее, чем никеля, а окиси атрия-очень слабое ( в 30 раз слабее никеля); ванадий увеличивает активность катализатора, а железо несколько компенсирует отрицательное действие других металлов при их постоянном содержании. Автор отмечает, что выведенное уравнение не претендует на точность. Оно только подчеркивает трудность создания подобных формул, которые бы учитывали все многообразные условия и причины, вызывающие отравление катализатора. Неточность уравнения автор объясняет: 1) ошибочными данными опытов, 2) неточностью некоторых данных, 3) неправильностью предположения о том, что каждый металл действует независимо от других металлов или что в сырье находится только один тип металла. Металлы, отложенные на катализаторе и находящиеся в сырье, вызывают различную степень отравления. [28]
Ситуация, когда диффузия лишь немного искажает истинную скорость реакции, весьма распространена. Второй предельный случай, когда скорость реакции определяется исключительно диффузией, мог бы осуществиться, как это видно из (8.3), при /) - - iCT5cM / ceK, R - - W - 8cM и К ж 10 - 12 - КГ11 см5 1 сек. Так как максимально возможное значение константы скорости реакции в газе vRz не намного больше, сомнительно, чтобы формула (8.3) была в этом случае точна. Неточность уравнения (8.3) связана с невозможностью точно экстраполировать уравнение диффузии на процессы, рпределяемые молекулярными размерами. До сих пор говорилось о стационарной скорости химической реакции, которая реализуется при определенном взаимном расположении молекул. Если молекулы распространены в пространстве каким-либо иным способом, скорость будет также отличной и зависящей от времени. Рассмотрим случай равномерного распределения реагирующих молекул в пространстве, когда оба типа молекул распределены по объему случайным образом. [29]
Страницы: 1 2