Неубывание - энтропия
Cтраница 1
Неубывание энтропии в изолированной системе обусловливается в конечном счете равновероятностью всех ее микроскопических состояний, приводящей систему в наиболее вероятное макросостояние. [1]
Эти уравнения необходимо дополнить условием неубывания энтропии, которое исключает появление неустойчивых разрывов. [2]
Однако в практическом смысле закон неубывания энтропии в изолированных системах не с чрезвычайно малым числом частиц является абсолютным. Его нарушение столь же невероятно, как, например, невероятно, что весь воздух некоторой комнаты самопроизвольно соберется в стакане, который стоит на столе. [3]
Уравнения газовой динамики необходимо дополнить условием неубывания энтропии в частице, выражающим второе начало термодинамики. Это условие приводит к тому, что в потоке газа могут существовать ударные волны т.е. такие линии разрыва функций w, 0, р, р, которые приводят к увеличению энтропии и плотности газа, но не существуют линии разрыва, за которыми энтропия и плотность потока уменьшаются. [4]
Ограничения на величину 6 в (49.7) следуют из условия неубывания энтропии на фазовом скачке. [5]
При всей тривиальности - это и есть качественная сторона неубывания энтропии. [6]
Подобные неравенства включают, например, часто используемое условие неубывания энтропии на разрывах без притока тепла. Это условие, очевидным образом, должно выполняться на разрывах, имеющих структуру. [7]
Можно показать [19, 34, 58, 65], что при выполнении некоторых достаточно общих требований ( непрерывности, неубывания энтропии при возрастании числа состояний, аддитивности) определение энтропии согласно равенству (16.2) является единственным. [8]
Это положение может быть использовано в качестве формулировки второго начала наряду с другим следствием закона неубывания энтропии, рассмотренным в § 10.2: теплота сама собой переходит только от более нагретых тел к менее нагретым. [9]
Таким образом, мы показали, что в ходе воображаемого процесса, противоречащего второму началу в формулировке Клаузиуса, энтропия убывает, что противоречит закону неубывания энтропии. [10]
Функции а, &, ip на некоторой характеристике второго семейства имеют разрыв класса Р1, если в точке разрыва выполнены соотношения (1.22) при некотором значении а, удовлетворяющем условию неубывания энтропии. [11]
Даже для простых задач, например для задачи о распаде произвольного разрыва, единственность решения (2.1) или (2.3) и (2.6) обеспечивается дополнительными условиями. В газовой динамике их роль выполняет требование неубывания энтропии при прохождении газа через ударную волну. [12]
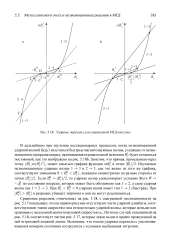 |
Ударные переходы для упрощенной МГД-системы. [13] |
Поэтому случай, показанный на рис. 5.18, соответствует частям рис. 5.17, которые лежат выше и правее проведенной на ней штриховой ломаной линии. Вспомним, что только ударные переходы с увеличивающимся номером состояния согласуются с условием неубывания энтропии. [14]
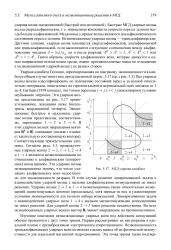 |
МГД ударная адиабата. [15] |
Страницы: 1 2