Неустойчивость - задача
Cтраница 1
Неустойчивость задачи (3.2) фактически порождена низким качеством модели, а формально может быть объяснена неустойчивостью операции псевдообращения. Более того, без дополнительных предположений задача редукции для возмущенной модели может оказаться неразрешимой. [1]
Неустойчивость задачи определения а тесно связана с так называемой плохой обусловленностью системы ( V-20) и главным образом матрицы В. Рассмотрим это понятие более подробно. [2]
Найдено условие неустойчивости одночастичной задачи для бозонов, движущихся в скалярном и электрическом полях. Решается задача о нахождении бозонного поля во внешних полях, превышающих критическое значение. Рассматривается конденсация бозонов в сильных скалярном и электрическом полях. [3]
Ниже выясняются условия неустойчивости одночас-тичной задачи для случая скалярного и электрического внешних полей, и определяется величина критического поля. [4]
Прежде всего выясним, как неустойчивость одночастич-ной задачи проявляется в теории поля. Рассмотрим сначала случай скалярных бозонов в скалярном внешнем поле. [6]
Найдем сначала для нескольких простейших случаев критические параметры внешнего поля, при которых наступает неустойчивость одночастичной задачи. [7]
Формулы числен но го дифференциро-в а н и я, в основе к-рых лежит И. Ввиду неустойчивости задачи численного дифференцирования относительно ошибок используемых значений функции в узлах шаг И. Поэтому на практике нередки случаи, когда известная с нек-рой погрешностью на густой сетке функция используется в данной задаче не во всех точках, а на более редкой сетке. [8]
Путем квазиреального эксперимента показано, что даже при высокой инструментальной точности прибс ров ( 6ех 0.05 %), регистрирующих спектр теплового излучения объекта, при аппроксимации зависимости е ( / параметрическими функциями, реально можно использовать всего несколько неизвестных параметров. Пр увеличении числа параметров возникает неустойчивость задачи по входным данным. Как уже отмечалось этим недостатком не обладают традиционные методы, используемые при теплофизических и метрологиче ских исследованиях е ( А) при высоких температурах. [9]
 |
Граф динамической системы. [10] |
В частности, непрерывность нарушается в точках, где числитель и знаменатель дробно-рациональной функции имеют хотя бы по одному близкому корню. Нарушение непрерывности обратного отображения приводит к неустойчивости задачи восстановления аналитического вида дробно-рациональной функции. [11]
Была выполнена большая серия модельных расчетов с различными ФР р (: г), в результате которых выяснилось, что во всех случаях величины уп - - 1, иными словами j обратная нелинейная задача, формулируемая в виде (10.42), устойчива. Тем не менее неустойчивость задачи, которая может проявиться в реальной ситуации при учете осложняющих ее факторов, устраняется с помощью стандартных методов регуляризации. [12]
Итак, мы нашли интервалы устойчивости ТЕд - и TEi-мод трехслойного нелинейного волновода, пользуясь известными результатами для задачи с одной границей раздела. Возмущение, приводящее к появлению TEi-моды, также деформирует дисперсионное соотношение, приводя тем самым к возмущению его корней, в результате чего у нулевого корня появляется малая мнимая часть, формирующая петли вокруг ( возмущенного) первоначального ненулевого корня - при этом вокруг значения t 1 / 2 возникает малая область неустойчивости, где корни комплексны. В итоге область неустойчивости расширяется, но не намного по сравнению с областью неустойчивости задачи с одной границей раздела. В области больших значений постоянной распространения мода будет устойчива. [13]
Как уже отмечалось, всякая задача при постановке на ЭВМ определяет совокупность вычислительных алгорифмов, отличающихся друг от друга порядком выполнения арифметических операций. Это означает, что точному решению задачи соответствует множество приближенных решений, которые могут быть получены с помощью таких алгорифмов. Среди элементов этого множества могут быть как близкие к точному решению, так и очень далекие от него. Разброс приближенных решений говорит о степени неустойчивости задачи к порядку выполнения операций. Рассмотренный пример суммирования чисел показывает, что даже в простейших задачах этот разброс бывает значительным. В более сложных случаях он может быть таким, что при некоторых порядках выполнения операций решение задачи на ЭВМ даже не может быть получено. [14]
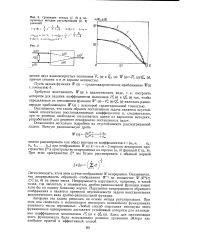 |
Сравнение точных ( /, 3 я полученных методом регуляризации ( 2, 4 решений. [15] |
Страницы: 1 2
