Структурная неустойчивость
Cтраница 1
Структурная неустойчивость или бифуркация подразумевает качественное изменение поведения решений системы при бесконечно малом изменении ее правой части. [1]
САР вносит структурную неустойчивость. Поэтому необходимо снижать порядок астатиз-ма. [3]
Возвращаясь к структурным неустойчивостям, рассмотрим несколько более подробно природу параметра порядка, необходимого для описания фазовых переходов, связанных с изменениями кристаллической структуры. Прежде всего структурные фазовые переходы происходят, когда в результате изменения каких-то внешних условий меняется симметрия кристалла. Так, при охлаждении ниже 393 К кристаллическая структура титаната бария превращается из кубической в тетрагональную. При непрерывных переходах параметр порядка описывает тип атомных смещений, ответственных за понижение симметрии. [4]
Некоторые материалы обладают свойством структурной неустойчивости: в них в ходе пластических деформаций наблюдаются фазовые превращения. Для таких материалов законы (3.30) - (3.32) нуждаются в некоторых поправках, которых рассматривать не будем. [5]
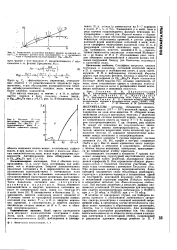 |
Зависимость положения верхнего уровня валентной зоны Ь л и нижнего уровня зоны проводимости а, от магнитного поля в бесщелевом полупроводнике Hgi - jMn Te. [6] |
V группы возникает вследствие структурной неустойчивости металла с простой кубич. Этот праметалл обладает ферми-поверхностъю с большими плоскими участками, размеры к-рых сопоставимы с размерами Бриллюэна зоны. При нормальных давлениях термодинамически более выгодной оказывается слабо искаженная ромбоэдрич. При высоких давлениях р металлич. Ее восстановление при всестороннем сжатии экспериментально наблюдалось у Bi ( Bill) при р 26 кбар, у Sb ( Sbll) при р 78 кбар. [7]
Неполное характеристическое уравнение всегда указывает на структурную неустойчивость, но наличие всех членов характеристического уравнения еще не означает, что система структурно устойчива. [8]
Прямым следствием теоремы является то, что структурная неустойчивость может быть установлена по одному из двух механизмов: в бифуркационном механизме зарядовое распределение имеет вырожденную критическую точку, тогда как конфликтный механизм характеризуется нетрансверсальным пересечением устойчивых и неустойчивых многообразий пар критических точек в зарядовой плотности. Теория катастроф может быть использована для математической модели структурных изменений в окрестности точки бифуркации путем анализа универсальных разверток, связанных с сингулярностями особых типов. [9]
Нарушение одного из этих неравенств приводит к структурной неустойчивости. [10]
Редко, однако, вопрос о стабилизации структурной неустойчивости системы решается так просто. Обычно разработчику приходите решать усложненную задачу - выбирать одновременно коэффициенты демпфирования и параметры регулятора в узких пределах возможности. [11]
Специальные случаи критических точек, отвечающих различным типам структурных неустойчивостей, рассматриваются в так называемой теории катастроф Тома. Мы здесь не останавливаемся на этой теории, но ее применение к некоторым специальным задачам биофизики представляется обещающим. [12]
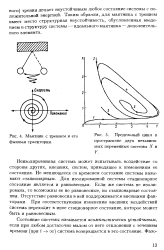 |
Маятник с трением и его фазовая траектория.| Предельный цикл в пространстве двух независимых переменных системы X и Y. [13] |
Таким образом, для маятника с трением имеет место структурная неустойчивость, обусловленная введением в структуру системы - идеального маятника - дополнительного элемента. [14]
Напомним, что в рассматриваемой задаче термины стабилиэируемость и структурная неустойчивость используются как эквивалентные. [15]
Страницы: 1 2 3 4
