Данная неустойчивость
Cтраница 1
 |
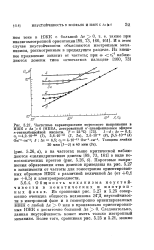
Профиль плотности заряженных частиц, при котором развивается диокотронная неустойчивость. 1 - распределение плотности, 2 - распределение скорости вращения. [1] |
Данная неустойчивость называется диокотронной. [2]
Данная неустойчивость электронного тока относительно ионов носит название неустойчивости Бунемана. [3]
Несмотря на существование многочисленных эволюционных расчетов с образованием петель, физическая природа данной неустойчивости и ее движущие силы остаются неясными. В [651] эта неустойчивость у массивных звезд с М & 15Af связывается с выходом водородного слоевого источника за скачок химического состава на границе максимального проникновения вглубь внешней конвективной зоны на предыдущих стадиях эволюции. Однако не исключено, что само это проникновение является следствием данной неустойчивости. Для менее массивных звезд предположения о физической природе петель отсутствуют. [4]
Как показано выше, точное описание нелинейных поляризационных эффектов требует одновременного учета как собственного линейного двулучепреломления, так и индуцированного нелинейного двулучепреломления. Данная неустойчивость проявляется в виде значительного изменения выходного состояния поляризации, когда входные мощность или состояние поляризации изменяются незначительно. В частности, явление поляризационной неустойчивости показывает, что медленная и быстрая оси световода, поддерживающего состояние поляризации, не полностью эквивалентны. [5]
Следовательно, данная неустойчивость может иметь только изотропный механизм. [7]
Здесь показано, что низкочастотные колебания могут быть неустойчивыми в зависимости от соотношения между v n / up и dn / Pd ПРИ заданной скорости UQ. Авторами [169] сделано предположение, что данная неустойчивость может быть причиной разогрева пылевого компонента, наблюдающегося в экспериментах при понижении давления нейтрального газа. [8]
Раскачка колебаний вторичным пучком должна быть наиболее эффективна на границе второго и третьего этапов, где ток вторичных электронов максимален. Из расчетов, аналогичных тем, которые были сделаны при обсуждении результатов ( 37 ], следует, что на границе второго и третьего этапов горит разряд, инициируемый вторичным электронным пучком. Существование данной неустойчивости в [23] объяснили тем, что плотность плазмообразующего газа вблизи поверхности металла определяется конкуренцией между подачей и расходом газа, а зажигание разряда увеличивает отток газа, поскольку ионы, движущиеся из разрядной области, имеют большую скорость по сравнению с нейтральными атомами. В [37] в условиях, близких к условиям [27], при использовании методов скоростной фоторегистрации наблюдали пульсации плазменного факела, поэтому можно сделать предположение, что в [27] пульсации тока мишени и давления газа обусловлены пульсациями плотности приповерхностной плазмы. Более того, можно предположить, что механизм этих пульсаций обусловлен неустойчивостью горения разряда за счет упоминавшегося выше эффекта ионной откачки. Однако непосредственное использование механизма ионной откачки для объяснения колебательной неустойчивости в [27] наталкивается на ряд трудностей. Поэтому скорость иоиов больше скорости нейтралов, причем в режиме ионной откачки поток ионов может на порядок превосходить поток подводимого в камеру плазмообразующего газа. Колебательная же неустойчивость в [27] развивается несколько в других условиях. Во-первых, в [27] отсутствует вблизи поверхности металла сильное продольное магнитное поле, поэтому ионы, как и нейтральные частицы, могут совершенно беспрепятственно уходить на стенки вакуумной камеры. [9]
Несмотря на существование многочисленных эволюционных расчетов с образованием петель, физическая природа данной неустойчивости и ее движущие силы остаются неясными. В [651] эта неустойчивость у массивных звезд с М & 15Af связывается с выходом водородного слоевого источника за скачок химического состава на границе максимального проникновения вглубь внешней конвективной зоны на предыдущих стадиях эволюции. Однако не исключено, что само это проникновение является следствием данной неустойчивости. Для менее массивных звезд предположения о физической природе петель отсутствуют. [10]
В дзухкомпонентном случае ( и более) это приводит к появлению в системе слагаемых, ответственных за перекрестную эффективную диффузию Заметим, что именно системы с такой диффузионной динамикой допускают возможность ДС - неустойчивости даже в отсутствие активной кинетики дислокаций. Проведенный синергетический анализ для этого случая показал, что при достижении в локальном объеме критических неравновесных условий, спонтанно образуется гексагональная дислокационная ячеистая структура, которая по мере увеличения степени неравновесности системы трансформируется в одномерно-неоднородную. Расслоение однородного состояния в рассмотренном случае обусловлено ДС-неустойчивостыо генерационно-рекомбинационного типа. При этом наличие двух компонент ( или более) в дислокационном ансамбле необходимо для реализации данной неустойчивости. В противном случае неустойчивость отсутствует. [11]
Эволюционные треки звезд с массами М, ЗМ на ГР диаграмме оказываются очень чувствительными к исходным параметрам и даже к методу численного счета ( § 32, пп. Столь нерегулярное поведение указывает на наличие тепловой неустойчивости, природа которой отличается от рассмотренных выше. Здесь имеют дело не с уменьшением г из-за изменения температуры, более того, темп ядерного горения здесь меняется слабо. Проявление данной тепловой неустойчивости состоит в неустойчивости эволюции звезды на стадии горения гелия в ядре и водорода в слоевом источнике. Математически это сводится к тому, что зависящие от времени решения уравнений эволюции оказываются неустойчивыми, т.е. сколь угодно малые различия в начальных условиях ведут со временем к большим различиям в решениях. В процессе развития данной неустойчивости соотношения между характерными временами г /, гг /, т по порядку величины не меняются. Неустойчивость является необходимым условием развития стохастичности [138], проявляющейся в численных расчетах. [12]
Страницы: 1