Номер - испытание
Cтраница 3
Приведенное здесь определение цепи Маркова является более узким по сравнению с определением § 1 гл. Здесь числа р у 1.3) ( (, / 1, 2, jii, N), являющиеся вероятностями перехода из состояния i в состояние /, не зависят от номера испытания, как в гл. Такие цепи Маркова называют однородными. Утверждение теоремы 1.2 верно только для однородных цепей Маркова. [31]
Величину Мт [ X ], которая, вообще говоря, тоже непредсказуема, называют эмпирическим средним случайной величины X ( s) для серии из m испытаний. Обращаем внимание на то, что в обозначениях непредсказуемых величин X ( s) и Мт [ Х ] у нас выписаны номера соответствующих испытаний, так как в эксперименте всякая измеряемая величина - и предсказуемая и непредсказуемая - появляется именно как функция от номера испытания. [32]
Колода карт, состоящая из 36 карт, сто раз была разделена наудачу на две равные части. В таблице 11 приведены результаты этого эксперимента. В первом столбце указан номер испытания, во втором - число появившихся в одной из полуколод красных карт, в третьем - число случаев деления красных и черных карт пополам среди уже произведенных испытаний и, наконец, в четвертом столбце даны значения частот. [33]
Эта Бернулли теорема была распространена С. Пуассоном ( 1837) иа случай последовательности независимых испытаний, где вероятность появления события А может зависеть от номера испытания. [34]
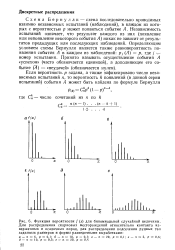
Схема Б е р н у л л и - схема последовательно проводимых взаимно независимых испытаний ( наблюдений), в каждом из которых с вероятностью р может появиться событие А. Независимость испытаний означает, что результат каждого из них ( появление или непоявление некоторого события А ] никак не зависит от результатов предыдущих или последующих наблюдений. Определяющим условием схемы Бернулли является также равновероятность появления события А в каждом из наблюдений: р / ( А) р, где / - номер испытания. [36]
Естественно возникает вопрос: какое отношение имеют найденные вероятности к реальным явлениям. Чтобы наглядно это ощутить, на одной из лекций был проведен такой эксперимент: студенты принесли несколько колод карт по 36 карт каждая и затем сто раз было произведено разделение колод наудачу на две равные части. В таблице 2 приведены результаты этого эксперимента. В первом столбце указан номер испытания, во втором - число появившихся в одной из полуколод красных карт, в третьем - число случаев деления красных и черных карт пополам среди уже произведенных испытаний и, наконец, в четвертом столбце даны значения частот. [37]
Теперь мы рассмотрим две фундаментальные теоремы теории вероятностей, имеющие обширный круг приложений. Обе эти теоремы представляют естественное обобщение уже известных нам теорем Я. В самом деле, представим себе наблюдателя, который после каждого испытания записывает результат его, ставя ( против номера испытания) 1 или О, в зависимости от того, появилось или не появилось событие в этом испытании. [38]
Особое внимание было уделено при этом классической теории безобидных игр. Мы могли видеть, в частности, что даже в том случае, когда математические ожидания существуют, участник безобидной игры может прочно занимать проигрышное положение. С другой стороны, анализ петербургской игры показал, что классическая теория применима также к некоторым играм с бесконечным математическим ожиданием, за тем исключением, когда безобидный вступительный взнос зависит от номера испытания. Следующая теорема выражает этот факт более точно. [39]
В этой измененной игре выигрыш имеет конечное математическое ожидание, равное N, и закон больших чисел применим. Следовательно, если игрок уплачивает перед каждым испытанием р / 0 рублей и повторяет игру) л раз, то при достаточно большом п он может быть уверен, что получит чистую прибыль. Это верно для каждого ( л /, но чем больше ji /, тем большим должно быть п, чтобы был вероятен положительный выигрыш. Классическая теория утверждала, что [ л / оо является безобидным взносом, но современный студент с трудом поймет невнятные рассуждения, приводившие к этому выводу. Оказывается вполне возможным определить взнос за право участия в петербургской игре таким образом, чтобы она имела все свойства безобидной игры в классическом смысле, за исключением того, что этот взнос будет зависеть от номера испытания, вместо того чтобы оставаться постоянным. Переменный взнос неудобен в игорном доме; однако петербургская игра и без того неосуществима вследствие ограниченности имеющихся денежных средств. Xk) 0 игра называется безобидной, если при больших п отношение общего выигрыша к общему уплаченному взносу епп. [40]
Страницы: 1 2 3