Номер - шаг
Cтраница 2
Верхний индекс ( п) означает номер шага итерации. [16]
Числа в квадратных скобках относятся к номерам шагов, а стрелки показывают направления изменения напряженного состояния на контакте при совершении очередного шага. Таким образом, из рис. 8.22 можно видеть, что до образования выработки касательное напряжение на элементе 10 ( см. рис. 8.21) равно нулю, а нормальное напряжение характеризуется точкой [0] на диаграмме Мора. Эта тенденция сохраняется до шага [8], на котором достигается предельное условие и происходит скольжение. Скольжение продолжается на шаге [9], и, наконец, на шаге [10] элемент раскрывается. Элемент 15 ведет себя точно так же, как элемент 10, за исключением того, что он не раскрывается. [17]
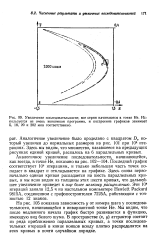 |
Увеличение последовательности. все серии начинаются в точке Не. Используется не очень экономная программа, и построение графиков занимает 5, 18, 20 и 202 мин соответственно. [18] |
На рис. 105 показана зависимость у от номера шага у последовательности, начинающейся в инвариантной точке Не. Мы видим, что после медленного начала график быстро развивается в функцию, имеющую вид белого шума. В пространстве ( х, у) аттрактор состоит из ряда приближенно параллельных кривых, а точки последовательных итераций в конце концов всюду плотно распределятся на этих кривых в почти случайном порядке. [19]
В этом случае гессиан не зависит от номера шага. [20]
Здесь индексы 2, 0 1 означают номер шага интегрирования, At - приращение времени, индекс г - номер обобщенной координаты или скорости. [21]
Эта формула может быть использована для определения номера шага, при котором достигается допустимое значение вероятности прогнозируемого состояния. [22]
Эта особенность предопределяет увеличение энтропии с ростом номера шага за счет выравнивания вероятностей всех возможных состояний внешней среды. [23]
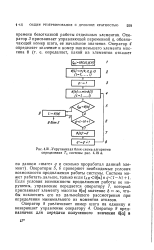 |
Укрупненная блок-схема алгоритма определения Гс системы а. [24] |
Оператор 3 присваивает управляющей переменной q, обозначающей номер шага, ее начальное значение. [25]
Система, сделав шаг gk, где k - номер шага, измеряет величину Fk и сравнивает ее с запомненным значением F /, на предыдущем шаге. В зависимости от знака приращения & Fk Fk - Fk-i следующий шаг А 1 производится в соответствующую сторону. [26]
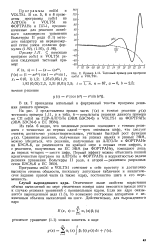 |
Пример Тестовый пример для программ voltsl и VOLTSL. [27] |
Отмеченное выше свойство нарастания объема вычислений по мере увеличения номера шага относится прежде всего к случаю решения уравнений с произвольным ядром. Если же ядро оказывается вырожденным вида (1.3), то возможно построение алгоритмов с неизменным объемом вычислений на шаге. [28]
В общем случае матрица ц [ может также зависеть от номера шага. [29]
При некоторых условиях в цепи Маркова с возрастанием k ( номера шага) устанавливается стационарный режим, в котором система § продолжает блуждать по состояниям, но вероятности этих состояний уже от номера шага не зависят. [30]
Страницы: 1 2 3 4