Нуль - передача
Cтраница 3
 |
Цепная схема четырехполюсника без взаимной индуктивности. [31] |
Покажем, что нули передачи совпадают с полюсами последовательных сопротивлений или нулями параллельных сопротивлений. [32]
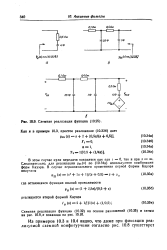
В общем случае нули передачи такого четырехполюсника имеют квадрантную симметрию ( рис. 18.13) вследствие четности ( нечетности) полиномов в числителях передаточных функций. [33]
 |
Схема реализации. [34] |
Теорема 7.2. Все нули передачи и полюсы передаточных функций лестничных LC-схем лежат на мнимой оси плоскости s, причем полюсы простые. [35]
 |
Схемная реализация функции. [36] |
В этом случае нули передачи находятся как при s 0, так и при s оо. Следовательно, для реализации 1 / 22 ( 5) по ( 1034а) используются комбинации форм Кауэра. [37]
Известно, что нули передачи цепных схем R, С обязательно расположены и а отрицательной вещественной оси. Следовательно, цепную реализацию нужно искать, когда все нули передачи - отрицательные вещественные. [38]
Если не все нули передачи данной передаточной функции лежат на отрицательной вещественной оси, то цепная схема не-реализуема. Здесь рассматривается случай, когда в отличие от условий синтеза по Фиалкову - Герсту нули передачи на положительной вещественной оси отсутствуют. [39]
 |
Схема реализации H ( s по. [40] |
Поскольку имеется два нуля передачи при s 0 и два - при s оо, нужно использовать комбинацию обеих форм Кауэра. [41]
При наличии нескольких нулей передачи получаемая цепь зависит от порядка реализации этих нулей, а также от того, какие полюсы используются для смещения нуля. Первый приводит к параллельной емкости, а второй - к резонансной параллельной ветви. Однако нет точного критерия для суждения о выборе полюса, за исключением того, что смещение нуля при полюсе в начале координат или бесконечности требует только один элемент, а при внутреннем полюсе - два элемента. [42]
Здесь имеется пара сопряженных нулей передачи, расположенных в левой полуплоскости, и отсутствуют нули на вещественной оси. Поэтому следует прибегнуть к помощи синтеза по Дашеру. [43]
 |
Пример предварительного искажения. [44] |
В приведеннном примере все нули передачи находятся в бесконечности. В более общем случае передаточная функция, соответствующая четырехполюснику без потерь с активной иа-грузкой, может иметь конечные нули, содержащиеся в четном или нечетном полиноме числителя. Таким образом, предварительно искаженная функция не может быть реализована в виде четырехполюсника без потерь с активной нагрузкой, а должна быть реализована как цепь R, L, С более общего типа в соответствии с результатами данной главы. [45]
Страницы: 1 2 3 4 5