Нумерация - вершина
Cтраница 1
Нумерация вершин во всех остальных столбцах осуществляется для вершин равного ранга последовательно, начиная с ( п - 1) - го. [1]
Нумерация вершин, начиная с индексных, разбивает матрицу W на два блока - неприводимого диагонального блока размера индекса и треугольного. [2]
Нумерация вершин дает возможность описать симметрии треугольника как перестановки вершин. Например, при повороте на 120 каждая вершина переходит в соседнюю по направлению против часовой стрелки. [3]
Нумерация вершин ГЧВ идентична нумерации вершин соответствующей СС и также позволяет получить матрицу смежности этих вершин, необходимую для построения графика. [4]
Нумерацию вершин можно осуществить более формально, не прибегая к вложению дерева в плоскость и используя обычное индуктивное построение деревьев с корнями. Для дерева, состоящего из одного ребра, такие пары вершин отсутствуют. Если дерево Т1 образовано из деревьев Т [ и Т2 в результате отождествления их корней, то одно из них ( например, TJ) объявляется ( по определению) левым, а другое ( Т2) - правым. Далее, в каждом множестве вершин, расположенных на одинаковом расстоянии от корня, эти вершины нумеруются слева направо, начиная с множества самых далеких от корня вершин. [5]
Нумерацию вершин зададим вектором w [ I: ml, где w Ш е М - истинный номер вершины, получающей t - й номер в этой нумерации. Нумерацию дуг мы задавать не будем, но введем вектор arc [ M ], сопоставляющий каждой вершине ( кроме первой) дугу с тем же номером. [6]
Нумерацией F вершин графа G называется пнъективное отображение множества вершин V ( G) графа в множество N натуральных чисел, F: V ( G) - - N. Иногда нумерация понимается в более широком смысле. [7]
При нумерации вершин метки не учитываются. [8]
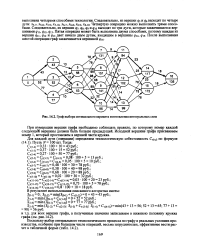 |
Граф выбора оптимального варианта изготовления интегральных схем. [9] |
При нумерации вершин графа необходимо соблюдать правило, по которому номер каждой следующей вершины должен быть больше предыдущей. Исходной вершине графи присваиваем номер 1, который проставляем в верхней части кружка. [10]
Способ нумерации вершин согласно алгоритму при указанном выборе значений функции удовлетворяет условию минимальности правильной граф-схемы. Поэтому оценка длины тренировочной последовательности / ( k - I) 2 справедлива также и для метода, доставляющего минимальные правильные граф-схемы. [11]
При этом нумерация вершин может быть произвольной, так как разным нумерациям соответствуют изоморфные алгебры. Приведенная нумерация согласована с каноническим базисом. [12]
При этом нумерация вершин может быть произвольной, так как разным нумерациям соответствуют изоморфные алгебры. [13]
При этом нумерация вершин может быть произвольной, так как разным нумерациям соответствуют изоморфные алгебры. Приведенная нумерация согласована с каноническим базисом. [14]
Пусть фиксирована нумерация вершин орграфа. Дуга называется обратной при этой нумерации, если она ведет от вершины с большим номером к вершине с меньшим номером. Построить такую нумерацию вершин заданного орграфа, при которой число обратных дуг минимально. [15]
Страницы: 1 2 3 4