Область - применение - уравнение
Cтраница 2
Наиболее изученной областью применения уравнения ( 5) является каталитическая зависимость Бренстеда ( разд. Как указал в 1924 г. Педерсен [2], константа К в этой зависимости не равна константе равновесия лимитирующей стадии переноса протона в рассматриваемой реакции, а лишь пропорциональна ей в силу термодинамической необходимости. Каталитические зависимости сыграли в истории химии очень важную роль, так как именно на их примере в 1924 г. было показано, что непрерывные математические функции могут быть использованы для описания по существу дискретного влияния изменений в строении реагента. Более значительные отклонения превышают вероятную ошибку эксперимента. Линейные логарифмические зависимости между влияниями структурных изменений на удельную скорость и константу равновесия одной реакции не ограничиваются реакциями переноса протона. [16]
Расширение области применения уравнения ( 4) учит нас, что это уравнение, указывая правильно и для любого рода движения числовую величину скорости, полностью скорость характеризовать все же не может. Действительно, для полной определенности необходимо указать еще и направление скорости. [17]
Чтобы оценить область применения уравнения ( 21), необходимо рассмотреть исходные предположения. [18]
Наиболее узкой область применения уравнения (7.71) становится для жидкометаллических теплоносителей вследствие весьма малых значений критерия Прандтля этих веществ. [19]
Хотя на практике область применения уравнения ( IX, 9) ограничена, как правило, вычислением AZ по АН, однако возможны случаи расчета величин теплот образования различных веществ но их изобарным потенциалам. [20]
Некоторое представление об области применения уравнения Гам-метта можно получить, рассмотрев приведенные на рис. 26 - 3 графики зависимости lg - г - от о для ряда различных реакций. [21]
 |
Зависимость произведения давления на молярный объем от давления [ PVm - f ( P ] для водорода и углекислого газа при О С. [22] |
Повышение температуры расширяет область применения уравнения состояния идеального газа, распространяя его действие и на более высокие давления. Из этого следует, что законы идеального газа могут быть использованы для обычных газов лишь при низких давлениях и высоких температурах. [23]
Следует указать, что область применения уравнения ВАХ (8.46) ограничивается для прямых смещений напряжениями, при которых еще существует потенциальный барьер перехода ( qV; ф0) и его сопротивление много больше сопротивления п - и р-областей полупроводника. Для обратных смещений это уравнение выполняется до напряжений, меньших пробивных. [25]
Увеличение занимаемого объема вначительно расширяет область применения уравнения состояния идеального газа к реальным газам. [26]
В работах К. Б. Яцимирского и сотрудников [59-74] была выяснена область применения уравнения Девиса для расчета термодинамических констант нестойкости и изучено влияние ионной силы на тепловой эффект. [27]
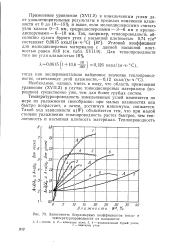 |
Зависимость безразмерных коэффициентов тепло - и температуропроводности от влажности. [28] |
Необходимо, однако, иметь в виду, что область применения уравнения ( XVII. [29]
Хотя Батлер и Поляни не сделали окончательного вывода о природе таких отклонений, их заслугой явилось а) расширение области применения уравнений Поляни - Эванса ( 1) и ( 20); б) выявление общей основы, которая позволяет осуществлять корреляцию термодинамических и кинетических характеристик превращений близких по строению органических молекул. [30]
Страницы: 1 2 3
