Область - метастабильное состояние
Cтраница 1
 |
Геометрическая интерпретация уравнения Ван-дср - Ваальса. [1] |
Области метастабильных состояний / и / / на рис. 36, а заштрихованы. [2]
Область метастабильных состояний сравнительно невелика; граница этой области на фиг. [3]
Область метастабильного состояния в смесях полимеров может охватывать достаточно большой интервал концентраций и обычно характеризуется резким изменением механических свойств. [5]
В учении о фазовых равновесиях области метастабильных состояний часто именуются областями расслоения или разделения на две фазы. В действительности сами процессы разделения на две фазы гомогенных систем, попавших в эти области, могут протекать чрезвычайно медленно. В особенности затруднено разделение на две фазы стеклообразных гомогенных растворов. Это необходимо еще и потому, что образование новой фазы из равновесных стабильных систем невозможно. Коллоидные частицы новой фазы могут возникать только в пересыщенных, метастабильных системах. Отчетливое понимание этого обстоятельства является основой для целеустремленного использования конденсационных методов получения дисперсных систем и дисперсных структур, в частности высокомолекулярных. [6]
Между спинодалью и бинодалью будет находится область метастабильных состояний. [7]
Область температур TI - Т2 оказывается областью метастабильного состояния. [8]
Для фазового превращения первого рода характерно существование области метастабильного состояния вблизи точки фазового превращения, например жидкость можно нагреть до температуры выше точки кипения или переохладить ниже точки замерзания. [9]
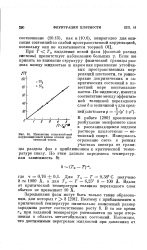 |
Изменение относительной корреляционной длины вблизи критической точки. [10] |
В то же время гк при заданной температуре уменьшается по мере вторжения в область метастабильных состояний. [11]
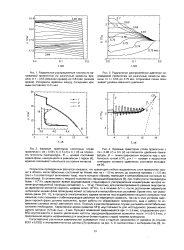
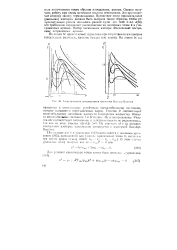
Результаты проведенных расчетов показали, что траектория любого выделенного слоя проволочки заходит в область метастабильных состояний не более чем на г - 20 не вплоть до момента времени t 5.6 мкс ( где t 0 соответствует включению тока), после которого образец переходит в метастабильное состояние во всем объеме. В соответствии с теорией гомогенного зародышеобразования [9], при темпе роста температуры более - 106 К / с характерное время формирования стационарного распределения концентрации центров кипения флуктуационной природы составляет тп - 10 не. Поскольку для рассматриваемого режима энерговклада характерной является скорость нагрева около 109 К / с, то в течение ДГ тп после достижения параметров на бинодали жидкая фаза проводника может оставаться в метастабильном состоянии. Кроме того, как указывалось ранее [10, 11], в процессе электрического взрыва металла под воздействием мощного импульса тока магнитное поле оказывает стабилизирующее действие на перегретую жидкость, так как в этих условиях зародыши паровой фазы должны выполнять, кроме работы по образованию поверхности, еще и работу по искривлению силовых линий магнитного поля. Поэтому в рассматриваемом случае учитывать - метастабильные состояния необходимо. Характерное время развития МГД неустойчивости для исследуемого режима можно оценить согласно [12] как TMHD - 2 мкс. Процесс плавления заканчивается при t - 3.8 мкс, следовательно рост МГД неустойчивости и резкое увеличение частоты зародышеобразования возможны после t - 5.6 - 5.8 мкс, и предложенная модель неприменима для описания более поздних стадий нагрева проводника. [13]
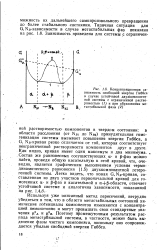 |
Концентрационная зависимость свободной энергии Гиббса в случае устойчивой двухкомпонент-ной системы с ограниченной растворимостью ( 7 и при образовании ме-тастабильной фазы ( 2. [14] |
Используя уже описанный метод пересечений, нетрудно убедиться в том, что в области метастабильных состояний химические потенциалы компонентов изменяются с концентрацией немонотонно и могут превышать свои стандартные значения Ц - А и ц, в. Поэтому промежуточным ( результатом распада метастабильНой системы, в частности, может быть выделение фазы чистого компонента, поскольку оно сопровождается убылью свободной энергии Гиббса. [15]
Страницы: 1 2 3 4