Анализ - каскад
Cтраница 1
Анализ каскада с коррекцией частотным методом ( в отличие от временного) с учетом Сн не вызывает принципиальных трудностей. [1]
При анализе каскада с ОЭ с действием емкости эмиттерного перехода Сэ можно не считаться, так как постоянная заряда этой емкости ( Сэгэ та) пренебрежимо мала. Не учитывается также влияние выходной емкости источника сигналов Сг. ОЭ достигает заметного значения. [2]
При анализе каскадов, на входе которых действует сигнал значительной амплитуды, необходимо использовать характеристики транзистора. [3]
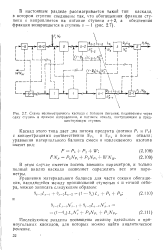 |
Схема несимметричного каскада с потоком питания, подаваемым через одну ступень в прямом направлении, и потоком отвала, поступающим в пред. [4] |
Последующие разделы посвящены анализу идеальных и прямоугольных каскадов, для которых можно найти аналитическое решение. [5]
 |
Переходные характеристики каскадов ОЭ.| Инвертор с токовым управлением. [6] |
Формула (3.6) пригодна для анализа каскада при любых формах входного тока цепи базы и нагрузках. Ее особенность состоит в том, что для нахождения выходного тока не нужно пользоваться величиной р, имеющей большой технологический разброс. [7]
 |
Активный четырехполюсник как обобщенная модель усилительного элемента. [8] |
Остановимся на основных линейных моделях УЭ, которые обычно используются при анализе каскадов предварительного усиления. Чтобы получить математическую модель УЭ, необходимо определиться с направлениями напряжений и токов. [9]
Следовательно, для описания усилительных каскадов на биполярных транзисторах можно использовать выражения, полученные при анализе каскадов на полевых транзисторах и наоборот с соответствующим преобразованием источника тока в источник напряжения. [10]
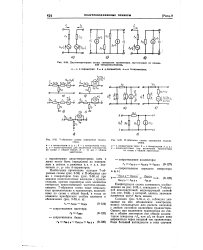 |
Двухгенераторные схемы замещения транзистора, вытекающие из уравнений четырехполюсника. [11] |
Наибольшее применение находят Т - образные схемы ( рис. 9 - 59) и П - образная схема с генератором тока ( рис. 9 - 60, а) при анализе низкочастотных каскадов с транзисторами, причем параметры всех элементов считаются вещественными частотно-независимыми. [12]
Рассмотрим работу каскада ОИ в ОНЧ. Анализ каскада ОИ в ОНЧ практически совпадает с анализом для каскада ОЭ. [13]
 |
Унисторный граф каскада с общим истоком. [14] |
Вместе с тем анализ каскада с помощью сигнального графа показал, что для определения его основных параметров не потребовалось составлять уравнения и решать их, а достаточно было записать только передачи сигнального графа от одной вершины к другой. [15]
Страницы: 1 2