Частотная область

Cтраница 2

Расчеты в частотной области с введением комплексной частоты получаются формально такими же, как и в цепях, состоящих только из У. В этом случае возможно производить анализ вынужденного режима при действии сигналов вида (7.62), частными случаями которых являются синусоидальные ( s / co), экспоненциальные ( s cr) и постоянные ( s 0) напряжения и токи. [16]

Умножению в частотной области соответствует свертка во временной области; другими словами, если ф и 02 являются масштабирующими функциями, то ф 02 также удовлетворяет уравнению масштабирования. Поэтому, отправляясь от 0о: Фнааг и используя рекуррентную схему фп 1: фо фп ( n 0), мы получаем последовательность все более регулярных функций, которые a priori удовлетворяют уравнениям масштабирования и по этой причине могут быть потенциально полезны при конструировании вейвлетов. [17]

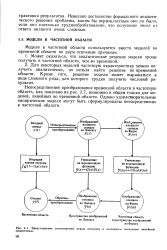Представление соотношений между входным и выходным сигналами линейной подсистемы. [18]

Модели в частотной области используются вместо моделей во временной области по двум основным причинам. [19]

Исследование этой частотной области требует микроскопического описания. Пример такого подхода приведен в разд. [20]

Свертку в частотной области можно вычислять, применяя ДПФ с использованием алгоритмов БПФ. Подобный алгоритм весьма эффективен и часто носит название высокоскоростной свертки. [21]

Планирование в частотной области для стационарного процесса оказывается более простым, чем во временной области, по следующим причинам. Поскольку для перехода в частотную область используется преобразование Фурье, то составляющие компоненты случайного процесса оказываются взаимно ортогональными. Это приводит к тому, что существенно сокращается размерность задачи, связанной с поиском минимума определителя дисперсионной матрицы оценок параметров. [22]

В обеих частотных областях эффективность впбровоздей-ствпя зависит от интенсивности механических колебаний, определяемых произведением амплитуды на частоту, характера затухания вибрационных импульсов в исследуемом материале и способа приложения воздействия. Здесь следует отметить, что реологические частотные характеристики полимерных материалов исследуются, как правило, в одномерных условиях, исследования пространственного затухания частотных импульсов в полимерных материалах проводятся весьма редко. [23]

При рассмотрении в частотной области, характеристики ( квази) интефатора и фильтра нижних частот не отличаются. [24]

Это условие в частотной области определяет зоны пропускания объемных волн в слоистых композитных материалах, распространяющихся перпендикулярно плоскостям раздела. [25]

При синтезе в частотной области, как правило, бывает задана амплитудно-частотная ( АЧХ) или фазо-частотная ( ФЧХ) характеристика. [26]

Формулы перехода от частотной области к временной, выраженные с помощью матриц. [27]

Существует неоднозначность в частотной области, связанная с отсчетами дискретных сигналов, которая отсутствует в мире непрерывных сигналов, и мы можем понять влияние этой неопределенности, разобравшись в природе дискретных данных. [28]

Имеются коэффициенты в частотной области а и ft для окна Хэннинга. [29]

При решении в вещественной частотной области с помощью преобразования Фурье предполагается, что входной сигнал интегрируем и цепь устойчива. [30]

Страницы: 1 2 3 4