Частотная область

Cтраница 4

В результате исследования в чисто частотной области порядок расчета, изложенный в настоящей главе по необходимости содержит анализ конструкции. В основном это связано с недостатком непосредственного изменения корней характеристического уравнения. Расчет коррекции путем анализа представляет косвенное приближение к решению задачи получения системы управления с удовлетворительным динамическим поведением. Этот способ является косвенным, потому что требуется определить корректирующую передаточную функцию, которая может создать требуемый предельный сдвиг фаз, а затем анализировать измененную систему для проверки достигнутых результатов. Когда результат не получился удовлетворительным, необходимо рассчитать измененную передаточную функцию и анализ повторить. Обычно требуется не более двух-трех попыток для получения корректирующей передаточной функции, которая дает заданный предельный сдвиг фаз; объем требуемых вычислений будет сравнительно небольшой при условии, что расчет производится по логарифмическим частотным характеристикам. В действительности подобные графики передаточных функций разомкнутых цепей и корректирующих контуров являются более наглядными, когда необходимо определить постоянные времени этих контуров с целью достигнуть необходимой коррекции. [46]

Среднеквадратичная амплитуда шума TN в частотной области является результатом суммирования вкладов всех пМ Мг накопленных в эксперименте точек временной области. [47]

Задача синтеза робастной системы в частотной области связана с определением такого регулятора Gc ( s), при котором чувствительность замкнутой системы была бы меньше некоторого допустимого значения, а минимизация чувствительности требует выбора такого регулятора, чтобы эта чувствительность была равна или достаточно близка к минимальному значению. Аналогично, задача обеспечения заданного запаса устойчивости по модулю связана с отысканием соответствующего регулятора, а максимизация запаса по модулю опять-таки требует выбора такого регулятора, при котором этот запас был бы наиболее близок к максимальному. [48]

Поведение линейной стационарной системы в частотной области [ р-области, р а / ( а, ( ш - fa) - комплексная угловая частота ] описывают с помощью передаточных функций, связывающих реакцию системы с ее возбуждением. [49]

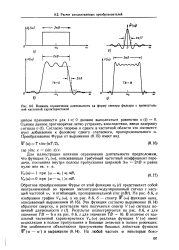Влияние ограничения длительности на форму спектра фильтра с прямоугольной частотной характеристикой. [50]

Согласно теореме о сдвиге в частотной области это соответствует добавлению к фазовому сдвигу слагаемого, пропорционального со. [51]

Если требуемая характеристика задана в частотной области, то функции а ( 0 и 9 ( 0 можно найти, преобразовав спектр во временную область. После этого, возможно, потребуется ограничить длительность сигнала и, кроме того, добавить короткие продолжения, чтобы устранить резкие разрывы. Так как ВШП по своей природе является дискретным, его частотный коэффициент передачи имеет основной максимум и ряд побочных лепестков на гармониках основной частоты. Будем полагать, что сигналу, заданному выражением (9.60), соответствует основной максимум частотного коэффициента передачи. В большинстве практических случаев побочные лепестки либо несущественны, либо могут быть подавлены за счет фильтрации. [52]

Этот рисунок иллюстрирует наложение в частотной области. Перекрывающаяся область, показанная на рис. 2.9, б, содержит ту часть спектра, которая перекрывается вследствие недостаточной частоты выборки. Из рис. 2.10 видно, что повышение частоты дискретизации f, позволяет устранить наложение путем разделения спектральных копий; результирующий спектр, показанный на рис. 2.10, б, соответствует случаю, приведенному на рис. 2.7, а. На рис. 2.11 аналоговый сигнал предварительно фильтруется, так что новая максимальная частота f m уменьшается до / / 2 или даже сильнее. Таким образом, поскольку fs 2f т, на рис. 2.11, б уже отсутствуют перекрывающиеся компоненты. Такой метод устранения наложения до дискретизации очень хорошо себя зарекомендовал в области проектирования цифровых систем. Отметим, что методы фильтрации, применяемые для удаления части спектра, в которой присутствует наложение, на рис. 2.11 и 2.12 приведут к потере некоторой информации. По этой причине частота дискретизации, ширина полосы среза и тип фильтра, выбираемые для конкретного сигнала, не являются независимыми параметрами. [53]

Было показано, как в частотной области выглядит свертка спектра сигнала со спектром косинусоиды. В данном разделе рассматривается обратный процесс. [54]

Страницы: 1 2 3 4