Стационарная область
Cтраница 1
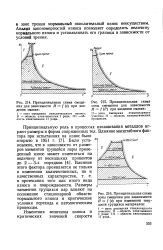
Стационарная область всегда связана с определенным видом трансформирования и разрушения ( износа) поверхностей трения. Этот вид трансформирования определяется динамическим равновесием процессов разрушения и восстановления вторичных структур. [1]
В стационарной области условий имеет место приблизительно линейная зависимость между тангенциальной и нормальной реакцией. Коэффициент пропорциональности в основном определяется механическими параметрами основного материала, рассеяние ( дисперсия) коэффициента пропорциональности - значением поглощенной энергии А. В этой области закономерно получение эмпирических зависимостей типа закона Амонтона - Кулона. [2]
В окончательной стационарной области можно выбрать такую калибровку, что электромагнитный потенциал А а будет там стационарен, а на J обратится в нуль. [3]
Для исследования окрестности стационарной области ( точки) уравнение ( 3) необходимо привести к каноническому виду. Для этого определяются собственные значения и собственные векторы матрицы, составленной из коэффициентов при квадратичных членах и членах, учитывающих парные взаимодействия. [4]
В то время как стационарная область у самых разных реакций примерно одинакова, периоды индукции и затухания протекают различным образом. Степень превращения в период индукции повышается обычно круто с началом трибохимической реакции. В период затухания скорость превращения может падать также очень круто или же, напротив, медленно. Наклон кривой зависит от вида реакции и от механической нагрузки. Реакции, которые во время механического воздействия проходят через состояния высокого возбуждения ( в терминологии модели плазмы - плазменные реакции), обнаруживают резкий подъем скорости превращения с началом механической обработки и такой же крутой спад с ее окончанием. [5]
Затем опыты проводят в стационарной области, и с ней связана разработка нелинейных моделей высших порядков. [6]
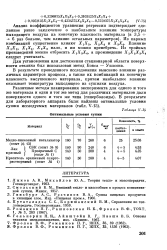 |
Оптимальные условия сушки. [7] |
Для установления или достижения стационарной области поверхности отклика был использован метод Бокса - Уилсона. [8]
Найдена математическая модель для описания стационарной области. [9]
Задача расчета экстремального плана эксперимента в стационарной области сводится к поиску некоторого плана е, дающего наилучшее приближение аппроксимирующих функций. [10]
Третье положение выделяет главные параметры в стационарной области условий трения. [11]
Главным объектом изучения теории внешнего трения является стационарная область нормального процесса. [12]
Первое условие вытекает из результатов экспериментального поиска стационарной области объекта. Предположим, что экспе - риментатор прекратил опыты, как только получил режим, удовлетворяющий всем ограничениям. [13]
Размеры элементов трущихся пар влияют на положение стационарной области нормального износа и критические условия перехода к патологическим процессам. [15]
Страницы: 1 2 3 4