Упругая область

Cтраница 2

В упругой области температура не меняется. [16]

Распределение напряжений в упруго-пластической области. [17]

В упругой области сг22 увеличивается от нуля на свободной поверхности надреза до некоторого значения и можно ожидать, что напряжения аХ1 ( и а33) также будут расти. [18]

В упругой области ( z z r) распределение перемещений в волокнах с точностью до постоянных интегрирования описывается выражениями ( 34) разд. [19]

В упругой области сохранение постоянства объема при деформации контролируется коэффициентом Пуассона. [20]

В упругой области, удовлетворяя условиям (2.5), (2.6) ( следуя [3], стр. [21]

В упругой области ( РРС), при ф О, величина К конечна, и, согласно (4.7), поле скоростей течения v ( r) спадает на расстояниях - л вблизи поверхности. При давлениях Р Рс длина К - ф 1 бесконечна и поле скоростей изменяется степенным образом в объеме кристалла. [22]

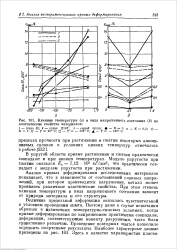Влияние температуры ( а и вида напряженного состояния ( б на пластические свойства материалов. [23]

В упругой области кривые растяжения и сжатия практически совпадают и при низких температурах. [24]

В упругой области для всех прокатных сталей модуль упругости составляет 2 06 - 105 МПа. При напряжениях от предела пропорциональности апц до ат модуль упругости уменьшается, что слабо сказывается на нарастании общих деформаций конструкций, но оказывает влияние на устойчивость сжатых элементов конструкций. [25]

В упругой области разность напряжений аг и 0е определяется константами упругости материала тСег, и величина деформации ЕГи / ао. [26]

В упругой области основное отличие деформации монокристалла и поликристаллического металла состоит в том, что монокристалл анизотропен, а поликристалл квазиизотропен. [27]

В упругой области деформаций действует закон Гука: а Е - е, где ст - напряжение, МПа; е - относительная упругая деформация; Е - модуль упругости материала, МПа. [28]

В упругой области напряжения не зависят от пути деформации и ее скорости и связаны только с величиной упругой деформации. [29]

В начальной упругой области, которая может быть как линейной, так и нелинейной, увеличение нагрузки заставляет точку, изображающую напряженно-деформированное состояние, двигаться вверх по кривой, а уменьшение нагрузки ( разгрузка) ведет к движению точки вниз по тому же самому пути. Таким образом, в упругой области существует взаимно однозначное соответствие между напряжением и деформацией. [30]

Страницы: 1 2 3 4