Сферическая область

Cтраница 2

Построение корректирующего тензора ( Тк) для сферической области / выполняется по схеме, рассмотренной в § 3, с учетом физико-механических свойств фиктивного тела. [16]

Вектор напряженности электрического поля в однородном диэлектрике внутри сферической области с радиусом R определяется выражением Е / гг, где г - радиус-вектор, проведенный из центра области до точки наблюдения. [17]

Расчеты по такому атмосферному блоку были произведены на условной сферической области ( в проекции Меркатора) с размером по долготе 120 ( с циклическим повторением), в которой в пределах широт 66 5 суша и море имеют одинаковые размеры, а по-лярнее ( до широт 81 7) имеется только суша. Модель успешно воспроизвела качественные особенности распределения компонент теплового и водного бюджета на поверхности Земли, в том числе распределение осадков с экваториальным поясом дождей и субтропическими пустынями, окаймленными поясом с малым количеством осадков, разорванным относительно дождливой областью вдоль восточного побережья континента. [18]

Эта формула вполне точна, если жидкость изотропна и сферическая область жидкости достаточно велика, чтобы ее можно было считать макроскопической. [19]

Подобная же процедура позволит нам построить функцию Грина для сферической области х2 у2 z2 R2 и получить решение задачи Дирихле для сферы. [20]

В этом случае линии тока ожижающего агента, расположенные внутри сферической области, радиус которой определяется из уравнения ( 4.11 - 30), замкнуты. Таким образом, рассматриваемая модель движения пузыря в псевдоожиженном слое также позволяет установить существование области замкнутой циркуляции газа, связанной с пузырем. [21]

Предполагаем, что для произвольной точки сферы вероятность попасть внутрь некоторой сферической области пропорциональна площади этой области. [22]

Лейтон [127] объединил принципы динамо в своей численной модели динамо в сферической области. [23]

Предполагаем, что для произвольной точки сферы вероятность попасть внутрь некоторой сферической области пропорциональна площади этой области. [24]

Учитывая сложную конфигурацию области возмущений разгрузки, разобьем ее на составляющие: сферические области / и область / /, форма которой зависит от вида загруженной поверхности тела. [25]

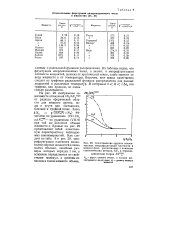Сопоставление средних относительных микрофлуктуаций плотности в жидкой фазе, рассчитанных с помощью статистических методов, 6NV и термодинамической теории 6WTePM. [26]

На рис. 29 изображены зависимости отношений 8ЛУ8Л те) М от радиуса сферической области для жидкого аргона, воды и ртути при состояниях, близких к тройной точке. [27]

В полиэтилене и каучуке ( без наполнителя) влага распределяется в виде разделенных сферических областей. В некоторых других материалах области влаги имеют форму сильно вытянутых эллипсов. Вследствие этого при одном и том же количестве влаги в материале получается разная зависимость тангенса угла потерь от частоты. [28]

Is - и 2s - AO для водорода. [29]

Различие между этими двумя орбиталями заключается в том, что для второй ор-битали имеется внутренняя сферическая область, где отсутствует электронная волна, плотность заряда равна нулю и вероятность нахождения электрона также равна нулю. Следует отметить, что для любого главного уровня, для которого главное квантовое число равно п, имеется п узлов, включая один при г оо ядра, где вероятность нахождения электрона, естественно, равна нулю. [30]

Страницы: 1 2 3 4