Анализ - корень
Cтраница 2
После вычисления численных значений коэффициентов ak каким-либо качественным способом анализа корней алгебраических уравнений, например путем построения ряда Штурма, необходимо установить количество вещественных и комплексных корней характеристического уравнения. В большинстве практических случаев рассматриваемое характеристическое уравнение имеет две пары комплексных сопряженных корней. [16]
После вычисления численных значений коэффициентов ak каким-либо качественным способом анализа корней алгебраических уравнений, например путем построения ряда Штурма, необходимо установить количество вещественных и комплексных корней характеристического уравнения. В большинстве практических случаев рассматриваемое характеристическое уравнение имеет две пары комплексных сопряженных корней. Поэтому положим Р; 2 - 6j / pj, Р3 4 - г / Ра и воспользуемся формулами Вьета, связывающими корни алгебраического уравнения с его коэффициентами. [17]
Для определения неустойчивости как конвективной, так и абсолютной, анализа корней одного дисперсионного уравнения недостаточно. [18]
Для линейного случая ( модель ARMAX) устойчивость модели может быть установлена путем анализа корней полинома С, в случае нейросетевой реализации провести анализ устойчивости модели значительно сложнее. Обычно устойчивость МНС-модели является локальной: NNARMAX-модель может быть устойчива в одном рабочем режиме и неустойчива в другом, что является существенным недостатком в случае практического применения. [19]
Если никаких ограничений на управление не наложено, то определение управления сводится к анализу корней некоторых функций. Оценки производных в этом случае получить не очень трудно, используя теоремы о неявных функциях. Если же на величину управления наложены ограничения типа неравенств, то задача качественно усложняется. Один и, возможных путей преодоления этой трудности состоит в использовании методов штрафных функгщй. [20]
Таким образом, метод малых колебаний предполагает линеаризацию уравнения движения ротора генератора, получение характеристического уравнения и анализ корней этого уравнения. [21]
 |
Характеристика мощности простейшей системы. [22] |
Выяснить характер переходного процесса, установить, устойчива или нет система при малом возмущении, можно, проведя анализ корней р 2 - Об устойчивости судят по знаку вещественной части корней. [23]
Алгоритмы, реализованные в программах РРМ и РР, обес нечивают расчет требуемого шага численного интегрирования на основе анализа корней ( полюсов) характеристического уравнения моделируемой системы. [24]
Поэтому математическая часть исследования как статической устойчивости, так и отыскания наилучших способов регулирования в основном сводится к анализу корней р характеристического уравнения. [25]
Все полученные выше основные соотношения, начиная с формул (7.107) и (7.108) сохраняют справедливость при комплексных проиицаемостях стержня и окружающей среды; при этом, разумеется, анализ корней уравнений (7.109), (7.111) и (7.112) оказывается в общем случае более сложным. [26]
Метод исследования малых колебаний относительно равновесного состояния позволяет свести задачу динамической устойчивости движения к задаче нахождения условий устойчивого решения системы линейных уравнений с постоянными коэффициентами и тем самым, по существу, свести решение к анализу корней соответствующего характеристического уравнения. В случае устойчивости движения корни этого уравнения должны быть в левой части плоскости Гаусса. Полином, обладающий такими свойствами, называется полиномом А. [27]
В МСС обычно находят не только закон движения u ( x, t) или ( х, t), но и компоненты тензора напряжений 8 з ( х, t) или Jij ( x, t) и др. Но для вычисления ттах надо вычислить главные напряжения QI, а2, аз и выбрать наибольшее из (6.45), что связано с решением и анализом корней кубического уравнения. [28]
Анализ корней этого уравнения показывает, что рассматриваемая система электропривода всегда устойчива. При этом двигатель действует демпфирующе на механические колебания. Параметром демпфирования является жесткость механической характеристики двигателя, которой определяется составляющая момента Д / И - ( ajk, пропорциональная скорости. Эта составляющая действует подобно скоростному ( вязкому) трению, преобразующему энергию колебания в тепло. [29]
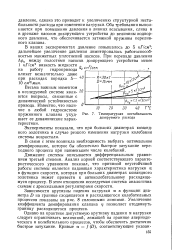 |
Температурная нестабильность дозируемого расхода. [30] |
Страницы: 1 2 3