Берр

Cтраница 1

Йоги Берра, импозантный кетчер New York Yankees, предупреждает: Если вы не будете знать того, куда вам идти, вряд ли вы сможете прийти куда-либо. [1]

Йоги Берра, легендарный бейсбольный принимающий из Янки, сформулировал происходящее одной фразой: Будущее теперь совсем не такое, как раньше. Он вполне мог бы добавить: Вы чувствуете, что за вашей компанией гонятся хищники. [2]

В таблице Стефана Берра ( рис. 109) представлены все графы с числом ребер не более шести. [3]

Каждый граф в таблице Берра может служить основой и для игры, и для задачи Рамсея, хотя найти критическую раскраску для критического графа ( т.е. решить задачу Рамсея) оказалось гораздо легче, чем найти критическую раскраску для классического числа Рамсея. [4]

Выделив нужные ферменты в чистом виде, Берр поместил их в пробирку вместе с плазмидами. Рест-рикционные ферменты незамедлительно напали на кольцевые плазмиды. Результатом этой атаки на ДНК явилась пробирка, полная длинных, нитевидных фрагментов плазмидной ДНК с липкими концами. Вообще-то говоря, липнут эти концы избирательно: они слипаются только с другими кусками ДНК, которые появились в результате действия того же рестрикциоиного фермента. [5]

На рис. 109 представлена ценная таблица, составленная Берром и опубликованная впервые мной в 1977 г. в разделе Математические игры журнала Scientific American. В ней представлены 113 графов с числом ребер не более 6 и без изолированных вершин, для которых известны обобщенные числа Рамсея. Обратите внимание на то, что некоторые из этих графов несвязны. В случае несвязного графа все его компоненты ( либо сплошь красные, либо сплошь синие) непременно порождаются полным графом с указанным в таблице числом Рамсея. [6]

График Ар-рениуса для термической деструкции полимера ( 45 в вакууме 6I. [7]

Термическая деструкция полиимидов на воздухе и в вакууме была изучена Бруком 59 - в1 и Хикоком и Берром 52 методом термогравиметрического анализа в области темпе - о во ратур 400 - 700 С. Было найдено, что ароматические полиимиды стабильны на воздухе 60 - приблизительно до 420 С, при более высоких температурах начинается их улетучивание. В вакууме ( 10 - 3 мм рт. ст.) эти полимеры показывают еще большую термостойкость, характеризующуюся отсутствием заметной потери массы при продолжительном выдерживании при температурах вплоть до 500 С. [8]

Хлопчатник Берра, зараженный двумя вредителями, был обработан препаратом фирмы Шервин-Уилльямс, хранившимся в бидонах с этикеткой DTOL 25 % emulsified. Часть распыленного препарата попала на соседнее поле хлопчатника, принадлежащее Пруэтту, сильно повредив этот посев, так же как и хлопчатник самого Берра. Вместо ннсекти - цида фактически применялся гербицид 2 4 - Д, опасный для двудольных растений, в частности для хлопчатника. [9]

Йоги Берра, импозантный кетчер New York Yankees, предупреждает: Если вы не будете знать того, куда вам идти, вряд ли вы сможете прийти куда-либо. Йоги Берра этого не знает. [10]

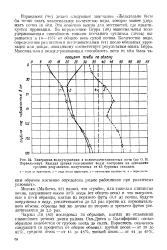Диаграмма водоудержяния и водоотдачи глинистых почв ( по. [11]

Израельсеи ( 80) делает следующее замечание Желательно было бы точно знать максимальное количество воды, которое может удержать почва in situ. Это особенно важно для местностей, где практикуется ирригация. По определению Берра ( 40) максимальная водо-удерживающая способность тонного песчаного суглинка ( лесса) выражается в 16 - 18 % от общего веса сухой почвы. Количество воды, определенное различными исследователями ( 81) после - обильных ирригации или дождя, невидимому соответствует результатам опыта Берра. [12]

Сложность задачи при переходе от Я ( 4, 4) к Я ( 5, 5) возрастает скачком настолько, что Стефан Берр, ведущий специалист по теории Рамсея, преподающий ныне компьютерные науки в колледже при Университете города Нью-Йорка, полагает, что это число может навсегда остаться неизвестным. По мнению Берра, даже число Рамсея R ( 4, 5) анализировать настолько трудно, что его значение может навсегда остаться неизвестным. [13]

Всякое ли положительное число, кроме 4 ( и, разумеется, единицы, что не имело бы смысла), является обобщенным числом Рамсея. В 1970 г. Харари показал, что ответ на этот вопрос утвердительный. В несуществовании обобщенного числа Рамсея, равного 4, нетрудно убедиться, рассматривая таблицу Берра. Тетраэдр ( полный граф с четырьмя вершинами) не может быть наименьшим графом, порождающим подграф, поскольку любой подграф тетраэдра имеет число Рамсея, которое либо больше, либо меньше четырех. [14]

Классическая теория Рамсея допускает множество поистине удивительных обобщений. Первопроходцами на этом пути были Вацлав Хватал и Харари, а глубоким изучением на протяжении последних 15 лет занимался Берр. Рассмотрим проблему нахождения чисел Рамсея для минимальных полных графов, которые непременно приводят к появлению монохроматической - конечной звезды. [15]

Страницы: 1 2