Оболочка - положительная гауссовая кривизна
Cтраница 1
Оболочка положительной гауссовой кривизны с двумя краями не имеет при т О изгибаний, если на каждом из ее краев задано хотя бы по одному закреплению. [1]
Для оболочки положительной гауссовой кривизны этот результат носит совершенно общий характер, схема расчета таких оболочек строится следующим образом. Сначала находится усилие в оболочке, которую представляют как тонкую, нерастяжимую мембрану, совершенно не сопротивляющуюся изгибу. Эта задача решается с помощью одних только уравнений статики и, собственно говоря, не относится к теории упругости. Соответствующая теория называется безмоментной теорией оболочек. Решение, найденное по безмоментной теории, как правило, не позволяет удовлетворить всем граничным условиям, поэтому вблизи границы рассматривается краевой эффект, связанный с изгибом. Ввиду малости области краевого эффекта, уравнения теории оболочек для этой области принимают относительно простую форму. Для вывода уравнений безмоментной теории нам понадобятся некоторые сведения из теории поверхностей, которые предполагаются известными и сообщаются для справки. [2]
Для формообразования оболочек положительной гауссовой кривизны применяют многие разновидности поверхностей двоякой кривизны. [3]
Статические условия работы оболочек положительной гауссовой кривизны позволяют создавать покрытия более экономичные, чем покрытия в виде оболочек других форм и в виде плоскостных конструкций. Экономическая эффективность таких оболочек связана с более рациональным ( с точки зрения работы материала) распределением в них усилий, с возможностью передачи на них значительных сосредоточенных нагрузок, что позволяет крепить подкрановые пути непосредственно к покрытию и тем самым снизить затраты на их устройство, с возможностью совмещения несущих, ограждающих и теплоизолирующих функций покрытия и, наконец, с лучшим использованием площадей и объемов сооружений. [4]
 |
Схема обжатия покрытия силами, приложенными по торцам контурных конструкций. [5] |
В покрытии с оболочкой положительной гауссовой кривизны и контурными фермами ( см. рис. 9.9, а) предварительное напряжение нижнего пояса фермы слабо вовлекает в работу решетку и верхний пояс фермы, а с ним и оболочку. В покрытии с контурными брусьями при обжатии его угловыми силами NO ( см. рис. 9.10, б) вместе с брусьями обжимается и оболочка. Решать эту задачу в общем виде достаточно сложно, поэтому ниже рассмотрено упрощенное решение. [6]
Если в качестве примера взять оболочку положительной гауссовой кривизны, на одну половину которой действует равномерно распределенная нагрузка q ( рис. 9.4, а), то, следуя правилам строительной механики, такое загружение можно рассматривать как сумму двух загружений по схемам симметричного и обратносимметрич-ного воздействия при половинном значении нагрузки в каждой схеме. [7]
Уже отмечалось, что в оболочках положительной гауссовой кривизны, загруженных нагрузками по всей поверхности оболочки, в угловых зонах образуются трещины. [8]
Особенности напряженного состояния сборных элементов рассмотрены на примере оболочки положительной гауссовой кривизны, квадратной в плане ( рис. 9.1), при этом предполагается, что она имеет жесткие контурные конструкции и нагружена равномерно распределенной нагрузкой. В схеме оболочки отмечены три типа сборных элементов с характерными погонными ( на единице длины сечения) силовыми воздействиями, которым они подвержены в составе оболочки. Имеется в виду, что сборные элементы окаймлены ребрами по периметру; стыкуются они между собой в углах с помощью стальных накладок, привариваемых к закладным деталям, которые предусмотрены в сборных элементах. Стыковые швы заполняются бетоном. [9]
Интересна система комбинированного покрытия, изображенная на рис. 11.3. Покрытие состоит из оболочки положительной гауссовой кривизны с плоским опорным контуром и периферийной пристройки с плоским балочным покрытием в сочетании с жесткими поперечными перегородками. В этой системе обращает на себя внимание наличие весьма жесткой контурной конструкции. Оболочка находится в особо благоприятных условиях работы, приближающихся к условиям работы купола с жестким опорным кольцом. [10]
Комбинированное покрытие, приведенное на рис. 6.6, б, образуется двумя пространственными покрытиями с оболочками положительной гауссовой кривизны и объединяющей их промежуточной короткой цилиндрической оболочкой, работающими совместно. [11]
В книге авторов из СССР и ГДР изложены основы проек-тирования железобетонных конструкций, имеющих покрытия с осесимметричными оболочками, оболочками положительной гауссовой кривизны, призматическими складками, цилиндрическими оболочками. Освещены вопросы совместного деформирования оболочек с контурными конструкциями, предварительного напряжения покрытия, оценки влияния ортотропности структуры и нелинейного деформирования бетона, условий монтажа на прочность возводимых конструкций. [12]
Если Г 0 ( положительная кривизна), то кривизны Ki ш К имеют одинаковый знак. К оболочкам положительной гауссовой кривизны относятся выпуклые оболочки. [13]
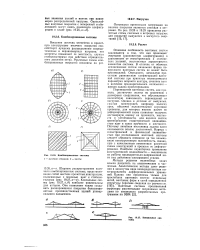 |
Комбинированные системы.| Консольные системы. [14] |
Перемещения вантовых систем, как правило, достаточно велики по сравнению с размерами сооружения, что обусловливает нелинейную зависимость перемещений от нагрузки. Однако в отличие от выпуклых, сжатых конструкций, например пологих арок, оболочек положительной гауссовой кривизны, для которых именно расчет по деформированной схеме позволяет получить достоверную оценку их прочности, жесткости и устойчивости, для висячих систем пренебрежение геометрической нелинейностью идет в запас прочности и жесткости. Поэтому линейная постановка задачи часто оказывается вполне достаточной. Наряду с геометрической и физической нелинейностью при исследовании Байтовой системы следует обращать внимание на так называемую конструктивную нелинейность, связанную с качественным изменением расчетной схемы конструкций в процессе ее деформирования. [15]
Страницы: 1 2