Оболочка - вращение
Cтраница 2
Оболочки вращения знакопеременной гауссовой кривизны могут быть двух видов. Подробнее эти вопросы здесь не обсуждаются. [16]
Оболочку вращения называют осесимметричной, если она нагружена равномерно распределенными относительно оси нагрузками. [17]
Оболочкой вращения называют оболочку, срединная поверхность которой образована вращением отрезка плоской кривой А В ( называемой образующей) вокруг прямой ss ( называемой осью поверхности), лежащей в плоскости АВ и ее не пересекающей. Каждая точка Р описывает при этом окружность радиусом г, называемую параллельным кругом, плоскость которого перпендикулярна оси. Плоскость, проходящая через точку Р и ось оболочки, пересекает последнюю по образующей или меридиану АВ. [18]
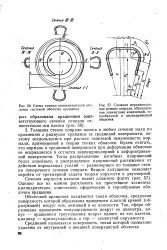 |
Схема замены несимметричной оболочки системой оболочек вращения.| Сложное меридиональное сечение спирали, образованное элементами конической, то-рообразной и цилиндрической оболочек. [19] |
Оболочкой вращения называется такая оболочка, срединная поверхность которой образована вращением плоской кривой ( образующей) вокруг оси, лежащей в ее плоскости. Так, сфера образована вращением полуокружности вокруг ее диаметра, конус - вращением треугольника вокруг одного из его катетов, цилиндр - прямоугольника, а тор - замкнутой окружности. [20]
Рассматривается оболочка вращения с гладким начальным профилем неотрицательной кривизны. Нагруже-ние считается простыми справедливой теория ( деформационная) пластичности. [21]
Для оболочки вращения с параметрами из предыдущего примера имеем следующее. Следовательно, для жестко закрепленной оболочки искривление ее образующей оказывает относительно меньшее влияние на критическую нагрузку по сравнению с шарнирно опертой оболочкой. [22]
Рассматривается оболочка вращения с гладким начальным профилем неотрицательной кривизны. Нагруже-ние считается простыми справедливой теория ( деформационная) пластичности. [23]
Для оболочки вращения нулевой кривизны вопрос о наличии изгибаний решается несложно, ибо семейство решений системы ( 2) можно выписать явно. [24]
Пусть оболочка вращения ненулевой гауссовой кривизны находится в условиях динамического нагружения. Напряженно-деформированное состояние оболочки характеризуется тензором кинетических напряжений ( Т), построение которого рассмотрим в настоящем параграфе. [25]
Расчет оболочки вращения при осесим-метричном нагружении наиболее простой. Такой подход может быть применен к более общим случаям нагружения, например, к оболочкам при несимметричном нагружении или неравномерном нагреве, а также к анизотропным оболочкам и оболочкам, имеющим переменную толщину и дискретные кольцевые подкрепления. Общая схема расчета при этом остается такой же. [26]
Для оболочек вращения разложением искомых функций в ряды Фурье по угловой координате оказывается возможным разделить переменные и свести задачу к системе обыкновенных дифференциальных уравнений, которые могут решаться численно обычными приемами с применением ЭВМ. [27]
Для оболочек вращения ( см. рис. 9.6) приведенные основные соотношения значительно упрощаются. [28]
Устойчивость оболочек вращения с изломом срединной поверхности / / Труды 18 - й Междунар. [29]
Расчет оболочек вращения при нестационарном взаимодействии с жидкостью / / Динам, и прочн. [30]
Страницы: 1 2 3 4