Составная оболочка

Cтраница 1

Покрытие с составной оболочкой из элементов отрицательной гауссовой кривизны. [1]

Составная оболочка под нагрузкой деформируется как единая пространственная система, образованная из отдельных элементов. Рассмотрение элементов без совокупного их взаимодействия ( что в некоторых публикациях предлагается делать ради упрощения решения) приводит к грубым искажениям реального напряженного состояния. Анализ напряженного состояния составных оболочек сложен; он еще недостаточно разработан. [2]

Составной оболочке отвечает кривая 3 - меридиан раскройной формы. [3]

Примеры конструктивных схем сборного составного покрытия а - вписанного в поверхность положительной гауссовой кривизны, с плоскими элементами складок. б, в - складчатого покрытия с косоугольными элементами скрученной формы при плоском опорном контуре и коньковом сопряжении в одной плоскости. / - прямоугольные элементы. 2 - косоугольные элементы. 3 - контурные конструкции. 4 - элементы складки скрученной формы. 5 - плоская горизонтальная опорная конструкция. 6 - коньковый горизонтальный брус. [4]

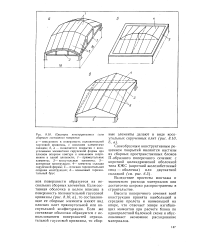
Если составная оболочка в целом вписана в поверхность положительной гауссовой кривизны ( рис. 8.10, а), то составляющие ее сборные элементы имеют вид плоских плит прямоугольной или косоугольной конфигурации. [5]

Для составной оболочки, разделенной на элементы, условия совместности в узлах внутренних элементов могут быть взяты в виде приравнивания ( с одной и другой сторон узла) величин б, f, N и Mpri что соответствует приравниванию величин 6, р, Н и Л1ф в случае осесимметричного нагружения оболочки. [6]

Прочность пологой составной оболочки с упругоподат-ливыми продольными швами / / Проблемы освоения нефтегазовых ресурсов Западной Сибири: Межвузовский сб. [7]

При составных оболочках целесообразно выполнять расчет промежуточных и краевых значений искомых величин как статически неопределимых систем, применяя формулы для краевых перемещений. [8]

Уравнение для составной оболочки с произвольным числом кольцевых ребер без труда составляется на основе приведенных соотношений. [9]

Схемы составной оболочки из двух коротких призматических складок, вписанных в цилиндрическую поверхность а - конструктивная схема. б - силы взаимодействия по границам четверти складки ( нагрузка, равномерно распределенная по всей поверхности оболочки. / - грань складки. 2 - контурные конструкции. 3 - полка сечения складки. 4 - ребро сечения складки. [10]

Изгибное состояние составных оболочек мало исследовано. Некоторые положения по изгибному состоянию складок и оболочек, изложенные выше в этой главе, справедливы и для составных оболочек. [11]

Уравнения для составной оболочки с произвольным числом кольцевых ребер без труда составляются на основе приведенных соотношений. [12]

Упругое равновесие составной оболочки спиральной камеры гидротурбины / / Прикл. [13]

Покрытия-настилы из сборных пространственных блоков с цилиндрической оболочкой ( а и с двускатной складкой ( б.| Комбинированные пространственные покрытия, состоящие. из длинной цилиндрической оболочки и двух плоских перекрытий пристроек ( а, из двух оболочек двоякой кривизны и промежуточной цилиндрической оболочки ( б 1 - длинная цилиндрическая оболочка. 2-бортовой элемент. 3 - диафрагма. 4 - плоское ребристое покрытие. 5 - ряды колонн. 6-торцовые стены продольных пристроек. 7 - оболочки положительной гауссовой кривизны. 8 - промежуточная цилиндрическая оболочка. 9 - контурные конструкции оболочки. [14]

Покрытия с составными оболочками осуществлялись многократно, в самых различных модификациях. Возможности их формообразования и конструктивных решений далеко не исчерпаны и в настоящее время интенсивно развиваются. [15]

Страницы: 1 2 3 4