Перекрестно армированная оболочка

Cтраница 1

Перекрестно армированные оболочки детально обсуждаются в гл. [1]

Детальный анализ перекрестно армированных оболочек дан в гл. [2]

Зависимость удельного усилия Т2 ( 1 и прогиба w ( 2 от осевой координаты. Нелнвениая теория ( - . линейная теория ( - . [3]

Дальнейший анализ напряженно-деформированного состояния перекрестно армированных оболочек проведем для полноты картины с позиций геометрически нелинейной теории, приняв и0 1 мм. [4]

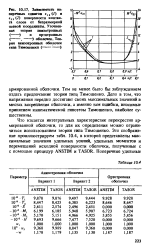Зависимость поперечных сдвигов е, СО и.. ( 2 поверхности контакта слоев от безразмерной осевой координаты. Уточненная теория анизотропных. [5]

Что касается интегральных характеристик перекрестно армированной оболочки, то для их определения можно ограничиться использованием теории типа Тимошенко. [6]

Дополнительную информацию о поведении двухслойной перекрестно армированной оболочки можно получить из рис. 10.9, где показана зависимость максимальных деформаций поверхности раздела слоев от угла армирования ус. Обратим внимание на величину тангенциальных сдвигов, которые выпадают из поля зрения при использовании теории ортотропных оболочек. [7]

Перекрестно армированная оболочка. [8]

Таким образом, при расчете перекрестно армированных оболочек, изготовленных из достаточно большого числа слоев, целесообразно использовать теорию ортотропных оболочек. [9]

Результаты решения задачи о растяжении двухслойной перекрестно армированной оболочки при ус 30 представлены на рис. 10.7. При численных расчетах было принято и0 1 мм. Как и следовало ожидать, учет нелинейности не приводит к сколько-нибудь значительному изменению силовых и кинематических характеристик оболочки. [10]

Определенный интерес вызывает картина напряженно-деформированного состояния перекрестно армированной оболочки с переменным углом армирования. [11]

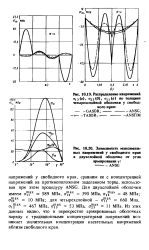Распределение нанрнжений 1з ( в. 23 (. и ( толщине четырехслойной оболочки у свободного края.| Зависимость максимальных напряжений у свободного края в двухслойной оболочке от угла армирования у. [12]

Из этих данных видно, что в перекрестно армированных оболочках наряду с традиционными концентраторами напряжений возникает значительная концентрация касательных напряжений вблизи свободного края. [13]

И Куликов Г.М. Концентрация напряжений у свободного края в перекрестно армированной оболочке / / XIV Всесоюзн. [14]

Так, пренебрежение влиянием мембранно-изгибных жесткостей ( в дальнейшем будем говорить об эффекте анизотропии) при расчете малослой-ных перекрестно армированных оболочек приводит к недопустимым погрешностям, искажающим напряженное состояние конструкции, особенно на границе раздела слоев. Исследование эффекта анизотропии сопряжено с большими трудностями даже в задачах осесимметричной деформации перекрестно армированных оболочек, так как в этом случае приходится интегрировать полную систему обыкновенных дифференциальных уравнений десятого порядка в теории оболочек типа Тимошенко и двенадцатого порядка в уточненной теории. [15]

Страницы: 1 2