Перекрестно армированная оболочка
Cтраница 2
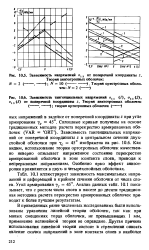 |
Заввсимость напряжений а, от поперечной координаты г.| Зависимость тангенциальных напряжений о, ( 1, агг ( 2. [16] |
Анализ данных табл. 10.1 показывает, что с ростом числа слоев в пакете до десяти традиционная методика расчета перекрестно армированных оболочек приводит к более лучшим результатам. [17]
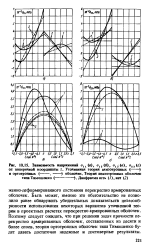 |
Зависимость напряжений а, ( в, а 2 ( б, а 3 ( в, о2Э ( г от поперечной координаты z. Уточненная теория анизотропных ( - . [18] |
Быть может, именно это обстоятельство не позволило ранее обнаружить убедительных доказательств целесообразности использования некоторых вариантов уточненной теории в проектных расчетах перекрестно армированных оболочек. Поэтому следует ожидать, что при решении задач прочности перекрестно армированных оболочек, составленных из десяти и более слоев, теория ортотропных оболочек типа Тимошенко будет давать достаточно надежные и достоверные результаты. [19]
На примерах цилиндрической и горообразной оболочек показано, что пренебрежение эффектом анизотропии приводит к количественно и качественно неверному описанию напряженно-деформированного состояния малослойных перекрестно армированных оболочек. [20]
Численные результаты, полученные с помощью процедуры ANSTIM, позволяют сделать следующие вьшоды: влияние анизотропии на напряженно-деформированное состояние малослой - HLJX перекрестно армированных оболочек существенно и пренебрежение эффектом анизотропии может привести как к количественно, так и качественно неверному описанию напряженно-деформированного состояния конструкции. Что касается многослойных перекрестно армированных оболочек, то при числе слоев в пакете более десяти учет анизотропии не существен и традиционные методы расчета будут давать хорошие результаты. [21]
Зависимость тангенциальных напряжений от поперечной координаты z в центральном сечении двухслойной оболочки при ус 45 изображена на рис. 10.6. Как видим, использование теории ортотропных оболочек качественно неверно описывает напряженное состояние перекрестно армированной оболочки в зоне контакта слоев, приводя к непрерывным напряжениям. Особенно ярко эффект анизотропии проявляется в двух - и четырехслойных оболочках. [22]
Численные результаты, полученные с помощью процедуры ANSTIM, позволяют сделать следующие вьшоды: влияние анизотропии на напряженно-деформированное состояние малослой - HLJX перекрестно армированных оболочек существенно и пренебрежение эффектом анизотропии может привести как к количественно, так и качественно неверному описанию напряженно-деформированного состояния конструкции. Что касается многослойных перекрестно армированных оболочек, то при числе слоев в пакете более десяти учет анизотропии не существен и традиционные методы расчета будут давать хорошие результаты. [23]
Быть может, именно это обстоятельство не позволило ранее обнаружить убедительных доказательств целесообразности использования некоторых вариантов уточненной теории в проектных расчетах перекрестно армированных оболочек. Поэтому следует ожидать, что при решении задач прочности перекрестно армированных оболочек, составленных из десяти и более слоев, теория ортотропных оболочек типа Тимошенко будет давать достаточно надежные и достоверные результаты. [24]
На практике оболочка нередко изготовлена из однонаправ-ленно армированных материалов, оси симметрии которых не совпадают с линиями главных кривизн исходной поверхности. Такая ситуация имеет место, к примеру, в перекрестно армированных оболочках. [25]
Так, пренебрежение влиянием мембранно-изгибных жесткостей ( в дальнейшем будем говорить об эффекте анизотропии) при расчете малослой-ных перекрестно армированных оболочек приводит к недопустимым погрешностям, искажающим напряженное состояние конструкции, особенно на границе раздела слоев. Исследование эффекта анизотропии сопряжено с большими трудностями даже в задачах осесимметричной деформации перекрестно армированных оболочек, так как в этом случае приходится интегрировать полную систему обыкновенных дифференциальных уравнений десятого порядка в теории оболочек типа Тимошенко и двенадцатого порядка в уточненной теории. [26]
Конструктивные особенности оболочек из композиционных материалов таковы, что вблизи свободных краев отверстий, зон межслойных дефектов может возникать значительная концентрация напряжений как нормальных, так и касательных. Эта проблема рассматривалась во многих работах [10.5, 10.8,10.12 -10.15] и, как правило, для пластин, подверженных действию растягивающих усилий. Здесь с помощью разработанных в книге процедур ANSTIM ( кинематическая гипотеза Тимошенко), TASOR ( обобщенная гипотеза Тимошенко), ANSG ( гипотеза ломаной линии), GASOR ( обобщенная гипотеза ломаной линии) дан сравнительный анализ кромочной концентрации напряжений в консольной перекрестно армированной оболочке. [27]
Страницы: 1 2