Безмоментная оболочка

Cтраница 1

Безмоментная оболочка представляет собой приближенную механическую модель реальной тонкостенной конструкции, в которой не учитываются внутренние изгибающие и крутящие моменты. [1]

Безмоментная оболочка может нести лишь тангенциальную краевую нагрузку, в соответствии с чем на ее рассматриваемом краю могут действовать лишь усилия Тг и S Т12, в которых, следовательно, и должно быть сформулировано краевое условие. Рассмотрим далее случай, когда граничные условия задаются в смещениях. [2]

Безмоментная оболочка не может быть нагруженной по своему краю ни перерезывающими усилиями, ни моментами. Углы поворота и нормальные смещения на ее краях не должны быть стеснены. Нарушение любого из перечисленных требований равносильно нарушению безмоментности напряженного состояния - в большей или меньшей мере. Однако, будучи необходимыми, эти требования не являются достаточными: помимо них имеются дополнительные условия, при нарушении которых безмоментное напряженное состояние не может существо-вовать. [3]

Безмоментную оболочку можно рассматривать как приближенную модель реальной оболочки, если в последней не учитывать изгибающие и крутящие моменты; безмоментная теория оболочек - это приближенная теория расчета, не учитывающая изгибающих и крутящих моментов; замена реальной оболочки безмоментной недопустима, если ее срединная поверхность при заданном способе закрепления может изгибаться без растяжений и сдвигов. [4]

Равнопрочная безмомент-ная оболочка вращения. [5]

Рассмотрим заданные безмоментные оболочки переменной толщины, определяемой таким образом, чтобы в каждой точке оболочки выполнялся принцип равнопрочности. Проектирование равнопрочной безмоментной оболочки удается выполнить достаточно просто, если в уравнения равновесия не входит толщина оболочки. В качестве примера таких объектов рассмотрим часто встречающиеся на практике оболочки вращения, находящиеся под действием внутреннего гидростатического давления. [6]

Уравнения безмоментных оболочек нулевой кривизны, к которым относится, в частности, система (8.6.2) - (8.6.5), изучены достаточно полно [ 6, 99, 322 и др. ] и их интегрирование не вызывает затруднений. [7]

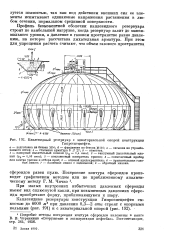Каплевидный резервуар с экваториальной опорой конструкции. [8]

Профиль безмоментной оболочки каплевидного резервуара строят по наибольшей нагрузке, когда резервуар залит до максимального уровня, а давление в газовом пространстве равно давлению, на которое рассчитана дыхательная арматура. [9]

В безмоментных оболочках могут развиваться большие деформации даже в тех случаях, когда они армируются семействами достаточно жестких волокон. [10]

Рассмотрим примеры расчета безмоментных оболочек. [11]

Погрешности аффинного моделирования безмоментных оболочек связаны со степенью воспроизведения условий существования безмоментного напряженного состояния в натуре и модели. Точность аффинного моделирования моментного напряженного состояния тонкостенных систем возрастает с увеличением степени пологости оболочки. [12]

Рассмотрим примеры расчета безмоментных оболочек. [13]

Интегрирование дифференциальных уравнений безмоментной оболочки нулевой кривизны не представляет труда и может быть выполнено в общем виде. [14]

Опорные связи в безмоментной оболочке могут быть только в касательных плоскостях к ее поверхности, так как составляющие опорных реакций, нормальные к поверхности оболочки, не воспринимаются последней. [15]

Страницы: 1 2 3 4