Анализ - прохождение - сигнал
Cтраница 1
Анализ прохождения сигнала через линейную цепь и преобразования в ней спектра сигнала основан на использовании амплитудно-частотной и фазо-частотной характеристик цепи. [1]
Анализ прохождения сигналов через линейные цепи, описываемые комплексной передаточной функцией, значительно облегчается при использовании методов контурного интегрирования на плоскости комплексной частоты р cr - f ко. [2]
Анализ прохождения сигналов череь инейные цепи состоит в исследовании возникающих в этих цепях переходных процессов, в результате которых происходит искажение параметров сигналов. [3]
Задача анализа прохождения сигналов через канал в полной мере решена тогда, когда по заданной и-мерной плотности распределения входного сигнала и оператору преобразования сигнала в канале найдена n - мерная плотность распределения выходного-сигнала. На практике используют и определяют более простые характеристики сигналов: одномерные и двумерные плотности распределения, корреляционные функции и спектральные плотности. [4]
При анализе прохождения сигналов через узкополосные системы, помимо перечисленных методов анализа, дающих точное решение, применяются приближенные методы, позволяющие для ряда задач получить решения, достаточно близкие к точным. На рис. 5.4 схематически представлена классификация методов анализа, которые рассматриваются в данной книге. Приближенные методы анализа ( методы огибающей, мгновенной частоты, приближенный спектральный метод) и примеры их использования рассмотрены в гл. Ниже приводится краткое изложение спектрального ( операторного) метода и метода интеграла наложения. [5]
С точки зрения анализа прохождения сигнала и шума рассматриваемый случай наиболее простой. Поскольку НЧ тракт является неискажающим устройством, то учитываться должны лишь масштабные соотношения. Для этого при расчете характеристик шума и сигнала на выходе НЧ тракта во все ф-лы, определяющие аналогичные характеристики на выходе детектора, вместо коэффициента / Сд вводится коэффициент ККяКвч, где Km - коэффициент усиления НЧ тракта. [6]
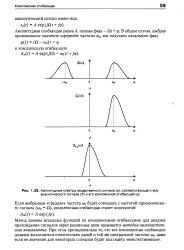 |
Амплитудные спектры вещественного сигнала ( а, соответствующего ему аналитического сигнала ( б и его комплексной огибающей ( а. [7] |
Метод замены исходных функций их комплексными огибающими для анализа прохождения сигналов через различные цепи называется методом низкочастотного эквивалента. [8]
Перечислим основные методы, с которыми приходится иметь дело при анализе прохождения сигналов через радиотехнические цепи. [9]
Напомним основные методы, с которыми приходится иметь дело при анализе прохождения сигналов через радиотехнические цепи. [10]
Соотношения (5.44) - (5.53) будут использованы в следующей главе при анализе прохождения сигналов через апериодический усилитель. Там же определим импульсную характеристику рассматриваемого усилителя. [11]
Напомним основные методы, с которыми приходится иметь дело при анализе прохождения сигналов через радиотехнические цепи. [12]
В течение последних приблизительно пятнадцати лет появились новые направления, а именно анализ прохождения сигналов через линейные и нелинейные пассивные и активные электрические цепи и синтез электрических цепей, создающих заданные формы выходных сигналов при известных формах входных сигналов. [13]
Итак, данная глава носит обзорный характер, чем и объясняются сжатое изложение и отсутствие конкретных примеров анализа прохождения сигналов через аналоговые системы. [14]
Если передаваемый сигнал s ( t) рассматривается как случайный процесс, что значительно приближает модели сигналов к реальным, то при анализе прохождения сигнала s ( t) через канал необходимо анализировать прохождение случайных процессов через четырехполюсники, описываемые различными операторами. Такие задачи решают в статистической радиотехнике [15], результаты решения этих задач находят непосредственное применение при анализе каналов передачи информации. [15]
Страницы: 1 2