Анализ - прохождение - сигнал
Cтраница 2
Анализ прохождения сигналов через нестационарные системы рассмотрен в § 6.6, где изучается влияние замираний сигналов на помехоустойчивость. Напомнил, что линейной называют систему, подчиняющуюся принципу суперпозиции. Работу линейной системы описывают с помощью дифференциального уравнения с постоянными коэффициентами. [16]
Задачи анализа прохождения сигналов через нестационарные системы рассматриваются в § 6.6, где изучается влияние замираний сигналов на помехоустойчивость. [17]
При анализе прохождения сигналов через линейные цепи наиболее часто используются следующие три метода: спектральный, операторный и временной. [18]
Для рассматриваемых в этой главе линейных систем с постоянными параметрами справедливы принципы суперпозиции и стационарности. Это сильно упрощает анализ прохождения сигналов через такие системы, позволяя использовать для этого различные характеристики, речь о которых пойдет в данном разделе. [19]
Ввэду Ограниченности объема подробные математические выкладки опускаются, а приводятся л ишь окончательные выражения ( и ( путь их получения. Прежде чем перейти к анализу прохождения сигналов - и - помех через отдельные элементы приемного устройства, рассмотрим вопрос о шум-а х в приемнике. [20]
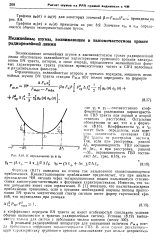 |
К определению Ъ и V. [21] |
Формула (8.17) выведена иа основе так называемого квазистационарного приближения. Квазистационарное приближение предполагает, что при анализе прохождения ЧМ сигнала через четырехполюсник можно пользоваться статическими амплитудно-частотными и фазовыми характеристиками. Известно, что такое допущение имеет свои ограничения. [22]
 |
Схема радиаль-но-упорного подшипника. [23] |
Солодова [42] посвящена теоретическим основам исследования линейных систем автоматического управления с переменными параметрами. Основные результаты, изложенные в монографии, относятся к анализу прохождения сигналов в виде заданных и случайных функций времени через систему с переменными параметрами. [24]
Очень часто математическое описание даже несложных по структуре детерминированных сигналов является весьма трудной задачей. Поэтому в теории электрических цепей и радиоэлектронике используется оригинальный прием, при котором реальные сигналы заменяют ( аппроксимируют, представляют, декомпозируют) набором идеализированных математических моделей, описываемых простыми функциями. Это дает важный инструмент для анализа прохождения сигналов через радиотехнические цепи. [25]
ВШП), наиболее часто используемых в качестве входных и выходных, в виде транс-нереальных ( цифровых) фильтров. Цифровые фильтры оперируют с сигналами, дискретизированными по времени и квантованными по уровню. Методы описания цифровых фильтров и анализа прохождения сигналов через эти фильтры находятся в тесной связи с существующими методами анализа аналоговых систем. Поэтому здесь мы рассмотрим только те соотношения между частотными н временными характеристиками цифровых фильтров, которые отличаются от рассмотренных соотношений для аналоговых систем и потребуются в дальнейшем при анализе работы ВШП н фильтров ПАВ. [26]
Теория дифференциальных уравнений с переменными коэффициентами значительно более сложна, нежели уравнений с постоянными коэффициентами. Поэтому ясно, что, хотя к линейным цепям с переменными параметрами и применим принцип наложения, спектральный подход к анализу прохождения сигналов через такие цепи не всегда оказывается эффективным. Более подробно этот вопрос освещен в гл. [27]
Интервал [, / г ] показывает время действия сигнала. При приближенном представлении сигналов набор чисел а & конечен. Основная задача - правильно выбрать системы ортогональных функций ( базис), удобные для анализа прохождения сигнала через цепи и каналы связи. [28]
Страницы: 1 2