Анализ - случайный процесс
Cтраница 3
В настоящее время одним из основных методов анализа случайных процессов служит корреляционная теория. Корреляционная теория позволяет при известных вероятностных характеристиках входа получить аналогичные вероятностные характеристики выхода. Следует еще раз подчеркнуть, что эти характеристики имеют смысл как характеристики множества процессов, а не отдельного процесса. Если, например, по дороге со случайными неровностями движется 1000 одинаковых автомобилей с одной и той же скоростью, то можно предсказать, в среднем, как данная дорога ( вход) действует на автомобиль: например, определить математические ожидания и дисперсии напряжений ( выход) в сечениях рамы автомобиля. Если же по ограниченному отрезку дороги движется один автомобиль, то получить вероятностные характеристики выхода ( без дополнительных предположений) нельзя. Еще более убедительным примером является одиночный старт ракеты ( см. рис. В. [31]
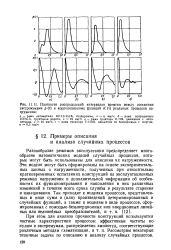 |
Плотности распределений интервалов времени между соседними экстремумами р ( т и корреляционных функций К ( т реальных процессов на-гружения. [32] |
Рассмотрим некоторые типичные задачи по описанию и анализу случайных процессов. [33]
Ниже рассмотрено несколько примеров, связанных с анализом случайных процессов при работе забойного двигателя и породе раз рушащего инструмента. [34]
Назовите причины, затрудняющие использование обычных преобразований Фурье для анализа случайного процесса. [35]
Данная книга посвящена общим проблемам интерпретации и применения результатов анализа случайных процессов прежде всего с помощью корреляционных и спектральных функций. Настоящая вводная глава представляет собой краткий обзор предмета, содержащий описание основных свойств случайных, процессов, рядов и интегралов Фурье и частотных характеристик физических систем. Более детальное изложение этих вопросов содержится в литературе, цитированной в конце главы. [36]
В связи с перечисленными неудобствами коррелированные отсчеты используют при анализе низкочастотных случайных процессов. [37]
Быстрое преобразование Фурье является единой алгоритмической базой для генерирования и анализа случайных процессов в цифровых системах подобно тому, как в аналоговых системах та же задача решается с помощью единой аппаратурной базы - узкополосных фильтров. В связи с этим большое значение имеет применение специализированных процессов БПФ ( см. рис. 6), которые позволяют на несколько порядков уменьшить время выполнения БПФ и ОБПФ по сравнению с программной реализацией этих алгоритмов в УВМ и, таким образом, существенно увеличить эффективность цифровых систем. [38]
Экспериментальное определение корреляционных функций является одним из наиболее распространенных видов анализа случайных процессов. [39]
Классическая теория колебаний ограничивалась детерминированными процессами, практически не уделяя внимания анализу случайных процессов. [40]
Экспериментальное определение корреляционных и взяимокорреляционнык функций является одним из наиболее распространенных видов анализа случайных процессов. Это объясняется не только важностью этих функции при решении многих задач техники связи, но и тем, что через данные функции выражаются и некоторые другие характеристики случайных процессов. [41]
Для решения некоторых задач по оценке нагруженности и расчету надежности конструкций представляет интерес анализ случайного процесса нагружения, который можно представить в виде сумм и произведений случайных стационарных и квази-детерминированных нестационарных процессов. [42]
В то же время она позволяет получить вторые центральный и начальный моменты, и для построения теории спектрально-корреляционного анализа случайных процессов вводить плотности вероятности более высоких порядков не требуется. [43]
В заключение нужно подчеркнуть, что коррелометры, основанные на методе аппроксимации, займут в дальнейшем видное место при анализе случайных процессов. [44]
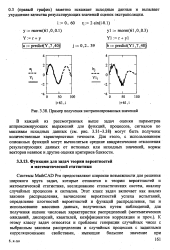 |
Пример получения экстраполированных значений. [45] |
Страницы: 1 2 3 4