Обращение - поле
Cтраница 1
Обращение поля в нуль в какой-либо точке пространства в определенный момент времени представляет собой инвариантный физический факт. Поэтому следует ожидать, что фаза р также будет инвариантом. [1]
Можно не требовать обращения поля в нуль на двух сторонах квадрата, а только предполагать, что случайные функции x ( t 0) и ж ( 0, s) с вероятностью 1 непрерывны. [2]
Хотя случай точечных зарядов вследствие обращения поля в этом случае в бесконечность в вычислительном отношении является не особенно удобным, мы все же рассмотрели его первым, имея в виду его ближайшее отношение к закону Кулона. Если заряды распределены в объеме с плотностью р, то соответствующая связь в формальном отношении становится гораздо проще. [3]
В то время ие были известны внезапные случайные обращения поля через интервалы в 103 - 107 лет, так что, по всем имевшимся сведениям, поле всегда имело современную величину и направление. [4]
Малые гистерезисные петли возникают в результате обращения поля в промежуточны. [5]
 |
У. Отставание напряжения от исчезает и диэлектрическая по-силы тока в идеальном диэлектрике стоянная имеет минимальное. [6] |
При промежуточных частотах и температурах:, когда период обращения поля того же порядка, что и время релаксации, ориентация отстает от поля. [7]
Одним из способов устранения спекл-структуры изображения является способ воспроизведения изображения при обращении поля через неоднородную среду, в качестве которой используется голо-графический рассеиватель. [8]
 |
Волновой фронт вол. [9] |
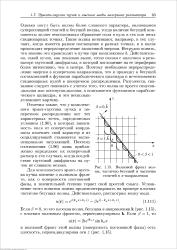
Однако могут быть волны более сложного характера, являющиеся суперпозицией стоячей и бегущей волны, тогда наличие бегущей компоненты делает невозможным обращение поля в нуль в тех или иных стационарных точках. Такие волны возникают, например, в тех случаях, когда имеется разное поглощение в разных точках, и в волне происходит перераспределение запасенной энергии. Действительно, такой пучок, как показано выше, тесно связан с наличием в резонаторе гауссовой диафрагмы, в которой поглощение на ее периферии более интенсивно, чем в центре. Поэтому необходимо перераспределение энергии в поперечном направлении, что и приводит к бегущей составляющей в функции параболического цилиндра и исчезновению стационарных нулей в поперечном распределении. Разумеется, сказанное следует понимать с учетом того, что волна не просто синусоидальная или косину соидальная, а описывается функциями параболического цилиндра, и это несколько усложняет картину. [10]
В [68] получены автомодельные решения для волновой области и показано, что скорость пересоединения может иметь любое значение вплоть до локальной альфвеновской скорости вне области обращения поля, так как конфигурации магнитного поля и потока плазмы могут взаимно подстраиваться. В [69] найдено, что максимальная скорость пересоединения обратно пропорциональна размеру диффузионной области. [11]
Действительно, если бы это условие не выполнялось, то происходило бы непрерывное движение зарядов вдоль поверхности, что невозможно ввиду предполагаемой статичности поля. Обращение поля в нуль внутри проводника и условие Et 0 на его поверхности однозначно определяют распределение заряда на поверхности проводника. [12]
Несколько лет назад Ранкорн [128] сделал замечательное и по тем временам весьма спорное открытие: остаточный магнетизм пород земной коры и, следовательно, геомагнитное поле в момент их кристаллизации претерпевали в прошедшие геологические эпохи внезапные обращения через каждый случайный интервал в 105 - 107 лет. Процесс обращения поля происходит быстро, всего за 103 лет или немногим дольше. [13]
Для стоячей волны характерно обращение поля в нуль в ее узлах. [14]
Теоретический анализ [104] показал, что при обращении поля плазма может быть устойчива вплоть до / 3 - 30 % относительно развития наиболее быстрых идеальных МГД-мод и до 17 % относительно тиринг-мод. [15]
Страницы: 1 2