Анализ - линейная цепь
Cтраница 1
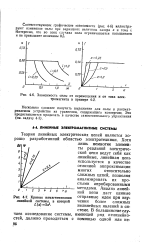 |
Зависимость силы от перемещения и от тока электромагнита в примере 4 - 2.| Кривые намагничивания линейной системы, в которой. [1] |
Анализ линейной цепи дает ценные отправные идеи при изучении более сложных нелинейных явлений в системе. [2]
Для анализа линейной цепи приложенный сигнал произвольной формы представляют, используя соответствующий математический аппарат разложения, в виде суммы элементарных составляющих, которые позволяют проводить анализ цепи более простым методом. Искомую реакцию цепи определяют наложением или суммированием элементарных реакций на действие каждой составляющей. [3]
При анализе линейных цепей применяют классический, операторный и суперпозиционный методы. [4]
Интегральный метод анализа линейных цепей с переменными параметрами впервые предложен Карсоном [163], изучившим отдельные системы первого и второго порядка. Согласно методу, обыкновенное дифференциальное уравнение системы с переменными параметрами заменяется интегральным уравнением Водь-черра второго рода. [5]
Известный символический метод анализа линейных цепей с неизменными параметрами, широко используемый в электротехнике и радиотехнике, может быть с большой пользой для общей теории входных каскадов радиоприемников также применен для анализа цепей с периодически изменяющимися пераметрами. [6]
Распространим символический метод анализа линейных цепей с постоянными параметрами на рассматриваемые двухполюсники с неоднородными синусоидально изменяющимися параметрами. [7]
Поэтому для упрощения анализа линейных цепей синусоидального тока можно применять различные методы расчета, которые были рассмотрены при анализе линейных цепей постоянного тока: метод преобразования цепей ( см. § 1.12), метод двух узлов ( см. § 1.13), метод контурных токов ( см. § 1.14), метод эквивалентного генератора ( см. § 1.17) и др. Для анализа линейных цепей синусоидального тока рассмотренные в гл. При этом математические формулировки различных методов расчета цепей постоянного тока остаются справедливыми и для расчета цепей синусоидального тока. Нужно только все ЭДС, напряжения и токи заменить комплексными значениями соответствующих синусоидальных величин, а сопротивления элементов - комплексными сопротивлениями. [8]
Теперь переходим к анализу линейных цепей в частотной области, который заключается в преобразовании систем интегро-дифференциальных уравнений в системы линейных алгебраических уравнений. Переменными в этих уравнениях являются не истинные токи и напряжения, зависящие от времени, а их преобразования или изображения, представляющие комплексные величины, зависящие от частоты. Анализ в частотной области позволяет ввести понятия сопротивления для индуктивного и емкостного элементов и тем самым формально свести расчет цепей с различными видами элементов к расчету резис-тивных цепей. [9]
Наряду с рассмотренными методами анализа линейных цепей часто используется временной метод ( метод интеграла наложения), заключающийся в отыскании отклика цепи с заданной импульсной характеристикой на произвольный сигнал. Под импульсной характеристикой цепи g ( t) подразумевается отклик цепи на воздействие, имеющее вид единичного импульса. [10]
С помощью программы GLEICH выполняется анализ линейной цепи постоянного тока, содержащей управляемые источники тока. [11]
Принцип наложения позволяет распространить результаты анализа линейных цепей при действии сигналов в виде ступенчатых или импульсных напряжений и токов на случаи действия сигналов произвольной формы. Здесь приводим так называемые интегралы наложения или свертки с использованием импульсной характеристики, с помощью которых можно найти реакцию цепи на действие сигнала любой формы и обойти трудности в определении вынужденных составляющих при сложных формах правой части уравнений. [12]
В книге рассматриваются современные методы анализа пассивных и активных линейных цепей во временнбй и частотной областях; особое внимание уделяется сущности процессов в цепи и фундаментальным понятиям, важным для изучения любых линейных систем. [13]
Ранее было показано, что при анализе линейных цепей приходится иметь дело с системами линейных алгебраических уравнений. Применение матриц для анализа цепей способствует лучшему пониманию свойств электрических цепей, а также позволяет получить некоторые более общие положения. [14]
МЭИ, 1986 ( программа предназначена для анализа линейных цепей в символьной форме. Позволяет рассчитать передаточную функцию в аналитической форме, АЧХ, ФЧХ, переходные процессы, осуществить оптимизацию. [15]
Страницы: 1 2 3