Математическое ожидание - ошибка
Cтраница 1
 |
Прохожде - ции я ( М входного сигнала найдем мате. [1] |
Математическое ожидание ошибки называется систематической ошибкой, ее среднее квадратическое отклонение - среднеквадра-тической ошибкой. Анализ качества систем управления сводится к определению указанных ошибок по вероятностным характеристикам случайных внешних воздействий. [2]
Математическое ожидание ошибки слежения равно ее среднеарифметическому значению. [3]
Система имеет математическое ожидание ошибки тст 0 и центрированную составляющую С, подчиненную нормальному закону распределения. [4]
Известно, что математическое ожидание ошибки уменьшается с увеличением частоты замеров и с уменьшением скорости линейного изменения коэффициентом. [5]
В этом случае математическое ожидание ошибки равно нулю. [6]
Учитывая, что при усечении математическое ожидание ошибки квантования отлично от нуля, более целесообразно использовать округление. [7]
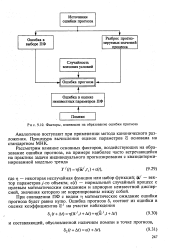 |
Факторы, влияющие на образование ошибки прогноза. [8] |
При совпадении ПФ с видом г математическое ожидание ошибки прогноза будет равно нулю. [9]
Получаемые вероятностные оценки поступают на сумматор 2, который определяет величину математического ожидания ошибок Мп для каждой из сравниваемых кодовых комбинаций. [10]
Формулы (5.5.12) и (5.5.14) характеризуют собой общие выражения соответственно корреляционной функции и математического ожидания ошибки положения для партии механизмов. [11]
При приеме в целом принятая кодовая комбинация будет ошибочной, если при математическом ожидании ошибок на ее длине Мл Мп mln и зафиксированное значение кодовой комбинации содержит любые варианты ошибок. [12]
Согласно соотношению ( 11) каждому из возможных состояний канала связи соответствует случайная величина математического ожидания ошибок Мс, которая через финальные вероятности состояний принятой модели может указать на наличие того или иного состояния с некоторой вероятностью правдоподобия рс. [13]
Чтобы упростить сравнение указанных методов, будем полагать, что первичные параметры взаимонезависимы, а математическое ожидание ошибок ( допусков) равно нулю. [14]
Функция потерь) в общем случае является функционалом от выходных сигналов объекта и модели или от математического ожидания ошибок оценок параметров. [15]
Страницы: 1 2