Определение - область - устойчивость
Cтраница 2
 |
Случай, когда v уменьшается во времени, а локальная температура увеличивается выше ее допустимого предела. [16] |
Аналогия между функциями и функционалами Ляпунова настолько велика, что можно поставить вопрос об использовании последних для систем с распределенными параметрами для определения области устойчивости в пространстве функциональных состояний. Такая возможность в случае систем с сосредоточенными параметрами была прямым следствием того, что замкнутые контуры в пространстве состояний единственным образом связаны с каждым значением функции Ляпунова. Кроме обеспечения устойчивости в малом существование семейства контуров Ляпунова гарантирует, что траектории не покинут определенную область в пространстве состояний. Для проверки справедливости этого утверждения в случае пространства функциональных состояний рассмотрим простое функциональное уравнение ( VII, 80) и заметим, что значение v соответствует площади под кривой профиля. [17]
Как было показано выше, при применении иммитанс-ного критерия абсолютной устойчивости не безразлично, что понимается под иммитансом: сопротивление или проводимость, так как неправильный выбор этой величины может привести к ошибке при определении областей устойчивости параметров цепи, не влияя на их границы. Во избежание таких ошибок следует рассматривать иммитанс той же размерности, какой обладает бесконечный иммитанс, делающий цепь устойчивой при его добавлении к выбранному контуру или узлу. [18]
Литературные данные о коррозии нержавеющих сталей в фосфорной кислоте имеются только для отдельных концентраций и температур. Для определения области устойчивости сталей марок Х18Н10Т ( ЭЯ-1Т); Х17Н13М2Т ( ЭИ-448) и ОХ23Н28МЗДЗТ ( ЭИ-943) в интервале концентраций от 1 до 116 % Н3РО4 при температурах от 80 до 170 С В. К. Огнева ( НИУИФ) провела необходимые исследования и построила диаграммы, показывающие зависимость постоянной скорости коррозии сталей от температуры и концентрации кислоты. На рис. IV-14 представлены линии постоянной скорости коррозии для значений 0 1; 0 25 и 0 5 мм / год. [19]
Впрочем, для определения области устойчивости вх ( т) достаточно указать только область параметров, при которых Qj ( т) ограничена. Множитель вида ехр [ Уг ( р) X ] при переходе во временную область определяет изменение Qi ( X, т) вдоль координаты X, а также запаздывание во времени, зависящее от координаты X, и поэтому на устойчивость не влияет. Слагаемые, стоящие в фигурных скобках выражения ( 11 - 8), являются однозначными функциями р и при значениях р, лежащих на окружности бесконечного радиуса в плоскости комплексного переменного р, остаются ограниченными. Это позволяет при переходе к временной области пользоваться замкнутым путем интегрирования в плоскости р и применять теорему о вычетах. [20]
 |
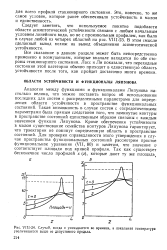
Амплитудно-фазовые и логарифмические частотные характеристики. [21] |
Данная задача может быть частично решена при помощи критериев построения граничных значений. Однако наиболее эффективно она решается методом определения областей устойчивости и неустойчивости. Если изменяется один параметр, область устойчивости определяется отрезками прямой. [22]
Исследование возможности замены функции запаздывания приближенным представлением для составляющих первого и второго порядков и определение минимального значения числа N этого представления, удовлетворяющего предъявляемым требованиям, будем вести в следующей последовательности. Сначала рассмотрим вопросы, связанные с определением области устойчивости и рабочих областей для составляющих первого порядка. Затем аналогичные вопросы будут изложены применительно к составляющим второго порядка. Одновременно будут даны некоторые пояснения по точности описания рабочих областей и переходных процессов для случаев точного и приближенного описания функции запаздывания. [23]
Этому значению со в плоскости 7, Тг соответствует не точка, а прямая, называемая особой. Если особые прямые не лежат целиком в бесконечности, то их надо нанести на диаграмме для определения областей устойчивости. [24]
Точкам пересечения с мнимой осью соответствуют некоторые критические значения коэффициента усиления, которые, как было показано, легко вычисляются с помощью критерия Рауса. Установление по корневому годографу одного или нескольких интервалов значений коэффициента усиления, при которых система устойчива, отвечает определению областей устойчивости в плоскости одного комплексного параметра с помощью метода D-разбиения. [25]
На самом деле динамические уравнения (5.63) являются только частью фундаментальной модели, составленной Зи-маном ( 1979); в этой работе можно найти подробное изложение модели и ее динамики. Наша цель состоит в том, чтобы привлечь внимание читателя к моделям такого рода и одновременно проиллюстрировать подход Ляпунова к определению областей устойчивости. [26]
Математическое моделирование позволяет решить основные задачи, возникающие при проектировании химических процессов, в частности - каталитических экзотермических процессов. К ним относятся: определение оптимального температурного режима в контактном аппарате, выбор оптимального состава газовой смеси на входе в реактор, расчет минимального времени контакта для обеспечения заданной степени превращения, определение области устойчивости процесса и др. Моделирование позволяет уменьшить объем опытных работ и сократить сроки пуска новых объектов. В настоящей работе рассматривается процесс получения окиси этилена - один из типичных экзотермических процессов. [27]
Математическое моделирование позволяет решить основные задачи, возникающие при проектировании химических процессов, в частности - каталитических экзотермических процессов. К ним относятся: определение оптимального температурного режима в контактном аппарате, выбор оптимального - состава газовой смеси на входе в реактор, расчет минимального времени контакта для обеспечения заданной степени превращения, определение области устойчивости процесса и др. Моделирование позволяет уменьшить объем опытных работ и сократить сроки пуска новых объектов. В настоящей работе рассматривается процесс получения окиси этилена - один из типичных экзотермических процессов. [28]
Правая часть формулы ( 11 - 8) есть сложная трансцендентная функция р и получить полную формулу для в ( т) не удается. Впрочем, для определения области устойчивости вх ( т) достаточно указать только область параметров, при которых вг ( т) ограничена. Множитель вида exp [ Yt ( p) X ] при переходе во временную область определяет изменение 0Х ( X, г) вдоль координаты X, а также запаздывание во времени, зависящее от координаты X, и поэтому на устойчивость не влияет. Слагаемые, стоящие в фигурных скобках выражения ( 11 - 8), являются однозначными функциями р и при значениях р, лежащих на окружности бесконечного радиуса в плоскости комплексного переменного р, остаются ограниченными. Это позволяет при переходе к временной области пользоваться замкнутым путем интегрирования в плоскости р и применять теорему о вычетах. [29]
При заданной структуре какие-либо параметры могут быть не фиксированными, т.е. их можно изменять. Такие параметры называют варьируемыми. При наличии варьируемых параметров возникает проблема определения области устойчивости. [30]
Страницы: 1 2 3