Определение - параметр - модель
Cтраница 1
Определение параметров модели, по существу, является искусством, а не логическим процессом, выраженным в виде совокупности определенных правил. Поэтому наиболее целесообразно проиллюстрировать методику определения параметров примером - и мы снова обратимся к исследованию электрического двигателя с механической нагрузкой. [1]
Определение параметров модели погрешностей - значений сй, с [ см. формулу (1.1) 1 и дисперсии случайной составляющей erg - осуществляется по логической схеме, представленной на рис. 1.4; вычисления по этой схеме иллюстрируются на примере. [2]
Возможно определение параметров моделей с застойными зонами и по одной С-кривой, зафиксированной в проточной зоне какого-либо промежуточного сечения данного аппарата. Очевидно, в этом случае отпадает необходимость в применении радиоактивных изотопов. При этом параметры моделей определяют по первым трем моментам экспериментальной С-кривой. Затем по экспериментальным значениям второго и третьего центральных или начальных моментов определяют параметры аи К. [3]
Для определения параметров модели разработан метод, позволяющий с высокой степенью точности оценивать эти параметры по моментам функции распределения. [4]
Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов. [5]
Для определения параметров более сложных гетерогенных моделей ( например, с учетом гидродисперсии) целесообразно использовать оптимизационный подбор с минимизацией некоторой функции качества. [6]
Методы определения параметров моделей рассматриваются в гл. Существо этих методов заключается в том, что на входе потока в аппарат наносится возмущение по составу потока путем введения индикатора и экспериментально определяется функция отклика на выходе потока из аппарата - кривая переходного процесса. В качестве индикаторов используются растворы солей и кислот, красители, радиоактивные изотопы. Обычно используются возмущения типа импульсного - в виде S-функции, ступенчатого, синусоидального или возмущения в виде случайного сигнала. [7]
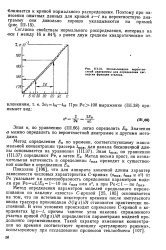 |
Использование вероятностной диаграммы для определения дисперсии функции отклика. [8] |
Метод определения параметров моделей продольного перемешивания по наклону хвоста С-кривой [25, 105] основывается на том, что по истечении некоторого времени после импульсного ввода трассера производная d ( gs) / dt становится практически постоянной. В этих условиях происходит спрямление С-кривой в координатах Igs - /, причем тангенс угла наклона спрямленного участка кривой d ( gs) / dt определяется параметрами моделей продольного перемешивания. [9]
При определении параметров модели по косвенным экспериментам встречаемся с еще одним весьма общим положением, одновременно ставя под сомнение безусловную выполнимость главного принципа и гордости науки, а именно принципа воспроизводимости как основы доказательности. Этот научный принцип четко сформулирован О. [10]
Однако для определения параметров модели не обязательно располагать общим выражением для функции распределения системы. Для этого достаточно иметь выражения для ряда числовых характеристик решения - моментов функции распределения, связь которых с параметрами модели значительно проще и удобнее для практических расчетов. [11]
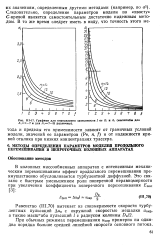 |
Графики для определения зависимости f от А - 7 и для / 1, 7 - 31 различны. [12] |
Следовательно, определение параметров модели по хвосту С-кривой является самостоятельным достаточно надежным методом. [13]
Затем необходимо определение параметров модели. Устанавливаются важность и влияние каждого из параметров на решение задачи. Необходима оценка их относительного влияния на систему в целом. В общем случае описание параметра должно содержать следующую информацию: определение и идентификатор параметра, единицу измерения, диапазон его изменения, характеристики ( однозначный-многозначный, регулируемый-нерегулируемый), место применения в модели, источник получения. [14]
Последующая процедура определения параметров модели очевидна. [15]
Страницы: 1 2 3 4