Определение - напряженно-деформированное состояние
Cтраница 2
Для определения напряженно-деформированного состояния пластины используется теория, основанная на гипотезах Кирхгофа-Лява. Деформация ребра описывается теорией Кирхгофа-Клебша. Деформации подкрепляющего ребра определяются на основе интегрирования дифференциальных уравнений изгиба и кручения отдельных элементов. Граничные условия для пластины сформулированы с помощью матриц податливости подкрепляющего ребра. [16]
Для определения напряженно-деформированного состояния подземного трубопровода используется численный метод, являющийся разновидностью метода конечных элементов, описанного в предыдущей главе. [17]
 |
Термо механическая поверхность материала. [18] |
Для определения неупругого напряженно-деформированного состояния теплонапряжекных конструкций при изменяющихся во времени температурах и нагрузках необходимо решать нелинейные задачи термопластичности и термоползучести. Если предполагать малость деформаций, то нелинейность является следствием соотношений, связывающих между собой напряжения и деформации в конструкционном материале и составляющих математическую модель этого материала. Необходимость применения той или иной модели материала обусловлена в основном характером действующих на конструкцию нагрузок и ее температурным состоянием. [19]
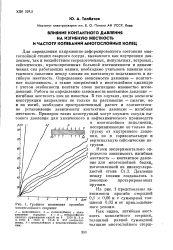 |
Графики изменения прогибов многослойного стержня. [20] |
Для определения напряженно-деформированного состояния многослойной стенки сварного сосуда, вызванного как внутренним давлением, так и воздействием сосредоточенных, импульсных, ветровых, сейсмических, кратковременных большой интенсивности и динамических сил работающих машин, необходимо учитывать влияние контактного давления между слоями на контактную податливость и из-гибную жесткость. Определению зависимости давление - контактная податливость, а также напряжений в многослойном цилиндре с учетом особенности контакта слоев посвящено множество исследований. Работы по определению зависимости контактное давление - изгибная жесткость нам не известны. В тех случаях, когда элементы конструкции направлены не только на растяжение - сжатие, но и на изгиб, необходим пространственный расчет и соответственно установление зависимости контактное давление - изгибная жесткость. [21]
 |
Диаграммы длительной прочности органического стекла при сложном напряженном состоянии При Т 20 С ( по В. П. Сдобыреву. [22] |
Методы определения напряженно-деформированного состояния с учетом ползучести материала были рассмотрены в гл. [23]
Задача определения напряженно-деформированного состояния трубы ( цилиндрической оболочки) в зонах расположения различных дефектов ( вмятин, коррозионных повреждений) представляется достаточно сложной для аналитического решения, так как параметры, характеризующие указанные дефекты, имеют случайный характер и плохо поддаются аналитическому описанию. Поэтому для решения этой задачи нами выбран один из современных численных методов - метод конечных элементов. В настоящее время он с успехом применяется для решения достаточно широкого круга задач в различных областях науки и техники. Практическая реализация МКЭ невозможна без использования ЭВМ. [24]
Задачу определения начального напряженно-деформированного состояния такого стержня будем считать решенной и закон распределения по длине стержня начальных сил N0 N0 ( х) известным. При достаточно малых значениях этих сил начальное состояние равновесия стержня с прямолинейной осью является единственным и устойчивым. Найдем условия, при которых это начальное состояние равновесия перестает быть устойчивым. [25]
Задача определения напряженно-деформированного состояния рассматриваемых соединений является более сложной, чем расчет подобных соединений без отбортовкн, как в теоретическом, так и в экспериментальном плане, Трудности расчетного анализа связаны со сложностью геометрии зоны сопряжения обечайки или днища с патрубком через отбортовку, резким изменением кривизны поверхности составной оболочечной конструкции. [26]
Задача определения напряженно-деформированного состояния твердого тела в общем случае внутренне статически неопределима, и для ее решения необходимо дополнить уравнения равновесия конкретными зависимостями между напряжениями и деформациями. Рассмотрим нелинейно упругое тело, у которого напряжения являются однозначными функциями деформаций, не зависящими от истории деформирования. Частный случай такого тела ( линейно упругого) был подробно описан в гл. [27]
 |
Зависимость сопротивления грунта от поперечных горизонтальных перемещений трубы. [28] |
При определении напряженно-деформированного состояния трубопровода, имеющего углы поворота в горизонтальной плоскости, необходима соответствующая расчетная модель грунта. Экспериментальные исследования, проведенные С. К. Гильзиным, показали возможность использования линейной зависимости между сопротивлением грунта и перемещением. Эксперименты проводились на трубах нескольких диаметров при различном расстоянии от боковой образующей трубы до стенки траншеи. Для этого диапазона перемещений зависимость близка к линейной. При аппроксимации полученных кривых линейной функцией можно отметить, что коэффициент нормального сопротивления грунта, равный тангенсу угла наклона прямой, тем меньше, чем больше диаметр трубы, что соответствует физической сущности явления. [29]
 |
Зависимость сопротивления грунта от поперечных горизонтальных перемещений трубы. / - при Он219 мм. 2 - при. н325 мм. 3 - при Кп 529 мм. [30] |
Страницы: 1 2 3 4