Определение - точка - бифуркация
Cтраница 1
Определение точек бифуркации и критических нагрузок энергетическим методом сводится к определению стационарных значений некоторых функционалов. Для решения последней задачи может быть применен метод Рэлея-Ритца. [1]
Для определения точек бифуркации пользуются способом Эйлера или энергетическим методом. [2]
Для определения точек бифуркации начального неискривленного состояния пластины следует рассмотреть искривленное изгиб-ное состояние равновесия пластины, бесконечно близкое к исходному. [3]
Основная идея определения точек бифуркации с помощью однородных линеаризованных уравнений состоит в следующем. Предположим, что одна какая-то форма равновесия системы известна и нужно найти точки бифуркации этой формы равновесия. Для этого достаточно, не интересуясь поведением системы вдали от известной формы равновесия, найти условия существования других форм равновесия, отличных от исходной, но бесконечно к ней близких. Те точки, в окрестностях которых существуют такие формы равновесия, и будут точками бифуркации. [4]
Основная идея определения точек бифуркации с помощью однородных линеаризованных уравнений состоит в следующем. Предположим, что одна какая-то форма равновесия системы известна и нужно найти точки бифуркации этой формы равновесия. Для этого достаточно, не интересуясь поведением системы вдали от известной формы равновесия, найти условия существования других форм равновесия, отличных от исходной / но бесконечно к ней близких. Те точки, в окрестностях которых существуют такие формы равновесия, и будут точками бифуркации. [5]
Кроме однородных линеаризованных уравнений, служащих для определения точек бифуркации, в теории упругой устойчивости широко применяют неоднородные линеаризованные уравнения для приближенного описания поведения систем с начальными неправильностями при малых, но конечных значениях отклонений. [6]
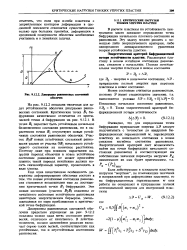 |
Диаграмма равномсных состояний оболочек. [7] |
В расчете пластины на устойчивость центральное место занимает определение точек бифуркации начального плоского состояния ее равновесия. [8]
В отличие от определения точки ветвления, в определении точки бифуркации заранее предполагается известным решение ( семейство решений), определенное при всех значениях параметра; речь идет об ответвлении решений от заданного. [9]
Если при этом полную потенциальную энергию подсчитывать в виде разложения по фг и ф2, то для определения точек бифуркации, видимо, не понадобятся высокие степени фг и фа. [10]
Исходное состояние равновесия, рассмотренной в предыдущем параграфе стержневой системы ( см. рис. 1.15) фг О и ф2 О известно. Для определения точек бифуркации нужно найти условия существования новых равновесных состояний, смежных с исходным. [11]
Исходное состояние равновесия, рассмотренной в предыдущем параграфе стержневой системы ( см. рис. 1.15) фх 0 и q2 О известно. Для определения точек бифуркации нужно найти условия существования новых равновесных состояний, смежных с исходным. [12]
При Ркр Р Р2 исходное состояние равновесия соответствует точке минимакса полной потенциальной энергии. Энергетический подход к определению точек бифуркации и критических нагрузок может быть применен и в более сложных случаях. Ркр полная потенциальная энергия в исходном неустойчивом состоянии не становится максимальной. [13]
При Ркр Р Ра исходное состояние равновесия соответствует точке минимакса полной потенциальной энергии. Энергетический подход к определению точек бифуркации и критических нагрузок может быть применен и в более сложных случаях. Ркр полная потенциальная энергия в исходном неустойчивом состоянии не становится максимальной. [14]
Иными словами - задача сводится к определению точки бифуркаций при достижении которой локальная неустойчивость переходит в глобальную. [15]
Страницы: 1 2