Соответствующий определитель

Cтраница 1

Соответствующий определитель получают отчеркиванием n - й строки и n - го столбца. [1]

Приравнивая нулю соответствующие определители шестого порядка, находим искомые характеристики и соотношения на них. Система ( 17) имеет три действительных семейства характеристик. [2]

Достаточно, чтобы соответствующий определитель 4-го порядка был отличен от нуля. [3]

При такой записи меняется знак соответствующего определителя. [4]

Аналогичным образом ( в виде соответствующего определителя четвертого порядка) может быть построена математическая модель системы ( п /) - групп. [5]

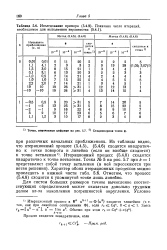Исследование примера. Показано число итераций, необходимое для выполнения неравенства. [6]

Для систем больших размеров точное вычисление соответствующих определителей может оказаться довольно трудным делом из-за накопления погрешностей округления. [7]

Нижние индексы при адъюнктах Аци означают, 4fo соответствующие определители вычисляются после вычеркивания строк и столбцов /, /, k в исходной матрице. Эти определители являются, следовательно, определителями порядка п - k, где k - число индексов. Они также могут быть вычислены по формуле разложения ( П-11), после того как определены новые избытки диагоналей в матрицах пониженного порядка. [8]

Определитель А - является транспонированным по отношению к соответствующему определителю из выражения (11.47), поэтому они численно равны. [9]

Полученное уравнение относительно X называется характеристическим уравнением, а соответствующий определитель - характеристическим определителем. [10]

Выбор зависимых переменных произволен, надо только, чтобы соответствующий определитель из элементов сц ( VII28) не был равен нулю. [11]

Первые четыре столбца в ( 46) линейно-независимы, ибо соответствующий определитель не равен нулю. Следовательно, набор из веществ ( СН4, Н2, Н20, СО) может быть взят в качестве базиса ключевых веществ. А поскольку они все измеряются, то на основании предыдущих результатов работы задача определения констант для данной системы имеет единственное решение. Матрицу С / Дх, х, k) не имеет смысла выписывать. Аналогичный вывод получен в [24] путем достаточно громоздкого расчета. [12]

Показать, что данные ниже функции линейно независимы, а соответствующие определители Вронского тождественно равны нулю. [13]

Число оборотов каждой из серии диаграмм Найквиста равно разности чисел нулей соответствующих определителей, и, таким образом, суммарное число оборотов серии диаграмм Найквиста равно разности чисел нулей в правой / ьполуплоскости главного1 определителя системы А и определителя А 1, а поскольку последний в правой / 7-полушюскости нулей не имеет, то числу нулей главного определителя А. [14]

Ясно, что возвратную разность можно определить и по графу, вычисляя соответствующие определители; при этом на структуру графа не накладываются никакие ограничения. [15]

Страницы: 1 2 3 4