Комплексная бифуркация
Cтраница 2
Решение этого уравнения дает нам значения переменной 0, после чего по формуле (5.5.14) нетрудно найти значения параметра Da, отвечающие точке комплексной бифуркации. [16]
Таким образом, мы получили систему обыкновенных дифференциальных уравнений (6.1.1), (6.1.2), (6.3.34) ( суммарно 12-го порядка) с 14 - ю граничными условиями (4.3.9), (6.3.35) - (6.3.37) и с двумя параметрами s, L, которые нам предстоит определить в точке комплексной бифуркации. Число уравнений согласовано с числом неизвестных, и описанную задачу можно пытаться решать либо с помощью разностных методов, либо методом стрельбы. Рассмотрим здесь оба этих подхода. [17]
Хопфа ( их называют также линии нейтральности. Наиболее интересными представляются те точки комплексной бифуркации, в которых ( при изменении одного параметра) меняется устойчивость стационарного решения. Если мы изменяем параметры ( 3 и а таким образом, что пересекаем указанную кривую точек комплексной бифуркации, то при этом изменяется устойчивость одного из имеющихся стационарных решений задачи. Мы можем построить также кривые точек комплексной бифуркации, в которых устойчивость стационарного решения не меняется - эти кривые позволяют судить о рождении неустойчивых периодических решений. [18]
Таким образом, мы имеем систему 2 ( п - 1) обыкновенных дифференциальных уравнений, для решения которой можно использовать методы, рассмотренные в § 5.5. Система ( 6.3.31 а, Ь) представляет собой некоторую аппроксимацию исходной распределенной системы. Поэтому описываемый подход применим лишь для не очень точного нахождения точек комплексной бифуркации, хотя в некоторых случаях даже при сравнительно большом шаге / г он дает вполне удовлетворительные результаты. [19]
Бифуркационная диаграмма для задачи 4 представлена на рис. 5.20 е в плоскости параметров 8 - а. В области, ограниченной кривыми вещественных бифуркаций, существует три решения, вне этой области - одно решение. Кривые комплексной бифуркации указывают нам на ответвление периодических решений и изменение характера устойчивости стационарных решений. В области единственности стационарных решений эти кривые выделяют область существования устойчивых предельных циклов. [20]
В точке z 0 мы получаем шесть нелинейных уравнений ( 6.3.40 а) и ( 6.3.42 а) относительно шести неизвестных t ] i, r) 2, r) 5, r) 6, s и Da. Эту систему можно решать методом Ньютона, причем матрица Якоби вычисляется с помощью уравнений в вариациях, либо исходя из соответствующих разностных формул. Пример сходимости метода Ньютона к точке комплексной бифуркации представлен в табл. 6.11. При этом соответствующие итерации сходятся к точке, которая лежит на ветви решений с высокой выходной степенью конверсии у ( 1) ( ср. Метод легко обобщается на задачи с большим числом уравнений, но размерность возникающих при этом ( конечномерных) задач, очевидно, возрастает. [21]
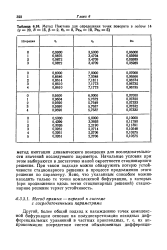 |
Метод Ньютона для определения точек поворота в задаче 14 ( Y 20, В 15, р 2, вс 0, Ре 10, Рен - б. [22] |
Начальные условия при этом выбираются в достаточно малой окрестности стационарного-решения. Ясно, что указанным способом можно находить только те точки комплексной бифуркации, в которых. [23]
Хопфа ( их называют также линии нейтральности. Наиболее интересными представляются те точки комплексной бифуркации, в которых ( при изменении одного параметра) меняется устойчивость стационарного решения. Если мы изменяем параметры ( 3 и а таким образом, что пересекаем указанную кривую точек комплексной бифуркации, то при этом изменяется устойчивость одного из имеющихся стационарных решений задачи. Мы можем построить также кривые точек комплексной бифуркации, в которых устойчивость стационарного решения не меняется - эти кривые позволяют судить о рождении неустойчивых периодических решений. [24]
Хопфа ( их называют также линии нейтральности. Наиболее интересными представляются те точки комплексной бифуркации, в которых ( при изменении одного параметра) меняется устойчивость стационарного решения. Если мы изменяем параметры ( 3 и а таким образом, что пересекаем указанную кривую точек комплексной бифуркации, то при этом изменяется устойчивость одного из имеющихся стационарных решений задачи. Мы можем построить также кривые точек комплексной бифуркации, в которых устойчивость стационарного решения не меняется - эти кривые позволяют судить о рождении неустойчивых периодических решений. [25]
Данная книга задумана прежде всего как справочное по-собие. Поэтому читатель не обязан стремиться изучить ее систематически от первой страницы до последней. Исходя из этого, некоторые основные определения мы повторяем в разных главах книги. Так сделано, например, при формулировке условий существования точки комплексной бифуркации ( бифуркации Андронова-Хопфа), и при изучении гл. Из-за ограниченности объема книги полностью соблюсти это правило не удалось, и потому ряд понятий и терминов в тексте приводится со ссылками на соответствующую главу, где это понятие вводится. В принципе каждую главу книги можно прорабатывать независимо от других. [26]
Устойчивость стационарного решения системы (5.1.1) характеризуется собственными числами матрицы Якоби, определяемой правыми частями соответствующих уравнений. Если мы изменяем один из параметров системы, то вдоль ветви решения на соответствующей диаграмме решений характер устойчивости может изменяться лишь в точках, где собственное число переходит из левой половины комплексной плоскости в правую. Переход вещественного собственного числа через нуль обсуждался нами в § 5.2. Если пара комплексно-сопряженных собственных чисел пересекает мнимую ось, то матрица Якоби все время остается невырожденной, и на диаграмме стационарных решений мы имеем регулярную точку данной ветви. Точки диаграммы стационарных решений, в которых пара комплексно-сопряженных собственных чисел пересекает мнимую ось, называются точками комплексной бифуркации1) или точками бифуркации Хопфа, по имени математика, опубликовавшего одну из основополагающих работ о характере решений в окрестности таких точек. Следующий существенный факт мотивирует разработку алгоритмов для нахождения точек комплексной бифуркации: в указанных точках ( при выполнении определенных условий) от ветви стационарных решений отходит ветвь периодических решений. [27]
Страницы: 1 2