Случайное блуждание - частица
Cтраница 1
Случайные блуждания частиц в двух - или многокомпонентных системах создают их перенос из области, где их химический потенциал больше, в область, где он меньше. Изменение химического потенциала может быть измерено лишь при переходе от равновесия к равновесию. Поэтому градиент химического потенциала следует рассматривать как псевдосилу, как макроскопический эквивалент микроскопических случайных событий. Смысл коэффициента a разъяснен на стр. [1]
Рассмотрим случайное блуждание частицы по целочисленным точкам действительной прямой, при котором частица на каждом шаге с равными вероятностями, смещается на 1 в положительном или отрицательном направлении. [2]
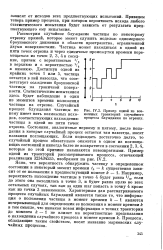 |
Пример одной из возможных траекторий случайного процесса блуждания по отрезку. [3] |
Рассмотрим случайное блуждание частицы по некоторому отрезку прямой, которое может служить моделью одномерного броуновского движения в области пространства, ограниченной двумя поверхностями. Частица может находиться в одной из пяти точек отрезка и через единичные промежутки времени перемещаться из точек 2, 3, 4 в соседние, причем с вероятностью V2 в верхнюю и с вероятностью V2 в нижнюю. Достигнув одной из крайних точек 1 или 5, частица остается в ней навсегда, что соответствует осаждению броуновской частицы на граничной поверхности. [4]
Происходит случайное блуждание частицы по точкам чис левой прямой AI, Аг, As, А с координатами 1, 2, 3, 4 соответствен но. Найти матрицу вероятностей переходов за 2 шага данной цепи Маркова. [5]
Рассмотрим случайное блуждание частицы по целочисленным точкам действительной прямой, при котором частица на каждом шаге с вероятностью п смещается на единицу вправо и с вероятностью q - 1 - p - на единицу влево. Пусть ( п) - положение частицы через п шагов. [6]
Рассмотрим случайное блуждание частицы, начинающееся в данном состоянии kq - kqi и после ряда состояний Jk. [7]
Диффузия является результатом случайных блужданий частиц, зависящих от температуры. Блуждания частиц ( броуновское движение) происходят и в однокомпонентных системах, где отсутствуют макроскопические градиенты концентраций. Броуновское движение в однокомпонентной системе не вызывает макроскопического потока. [8]
Уравнение Фоккера - Планка описывает случайное блуждание частиц, и такой вид асимптотики на больших временах означает, что после нескольких столкновений броуновская частица забывает начальные условия. [9]
Покажем теперь, как практически возможно организовать случайное блуждание частицы с заданными вероятностями перехода ру. [10]
В заключение вернемся к рассуждению о характеристиках случайного блуждания частицы на прямой, помещенному в конце § 5 гл. Там речь идет о характеристиках блуждания: среднем значении пробега и среднем квадратическом отклонении от среднего пробега. [11]
Рассмотрение механизма конвективной диффузии основано на понятии случайного блуждания частицы индикатора. [12]
Радиальное рассеяние происходит в соответствии с предсказаниями теории случайного блуждания частиц. Твердый элемент насадки делит набегающую струйку потока, отклоняя ее в радиальном направлении, причем порции жидкости по отношению к соседнему элементу насадки отклоняются внутрь или наружу с равной вероятностью. [13]
Выбирая последовательность случайных чисел и руководствуясь указанным выше правилом, получаем случайное блуждание частицы с фиксированным начальным состоянием и данными вероятностями перехода. Для достижения нужной точности корней ( в вероятностном смысле) следует рассмотреть достаточно большое количество независимых блужданий. [14]
В обычных процессах диффузии случайность есть не что иное, как случайные блуждания частиц жидкости. Примером могут служить нерегулярное тепловое движение молекул в жидкости. [15]
Страницы: 1 2 3