Пентатоп
Cтраница 1
Пентатоп проектируется при этом на каждую из координатных плоскостей в форме, более удобной для обзора и практического использования. Хотя отдельные его части могут быть сжаты в различной степени и даже до нуля, общий смысл полученных проекций существенно иной, чем тот, который получается при пользовании обычным методом Буке. [1]
Пентатоп можно представить себе как геометрическую фигуру, полученную из тетраэдра, на каждой грани которого в четырехмерном пространстве построены тетраэдры, имеющие общую вершину. Пентатоп, следовательно, ограничен пятью тетраэдрами, подобно тому, как, например, тетраэдр ограничен четырьмя треугольниками, а треугольник - тремя сторонами. [2]
Пентатопы, включающие свободные вершины, образуют боковые ветви ( отростки) в цикле пентатопов. [3]
Пентатопы, включающие свободные вершины, образуют боковые ветви ( отростки) в цикле пентатопов. Далее для нахождения остальной ( внутренней) части сингулярной звезды необходимо найти базисный треугольник, построенный из трех наиболее стабильных диагоналей; таковыми является треугольник V2Li2SO4 - NaCl-TIBr ( рис IIЛ, б), который служит общим основанием для четырех остальных секущих тетраэдров. [4]
Пентатоп перемещается в направлении пятой оси OR, точка F - одна из вершин образовавшегося полиэдроида - гексатопа ABCDEF. [5]
Пентатоп можно представить себе как геометрическую фигуру, полученную из тетраэдра, на каждой грани которого в четырехмерном пространстве построены тетраэдры, имеющие общую вершину. Пентатоп, следовательно, ограничен пятью тетраэдрами, подобно тому, как, например, тетраэдр ограничен четырьмя треугольниками, а треугольник - тремя сторонами. [6]
Ни пентатоп, ни тетраэдрический гексаэдроид не имеют такого числа вершин, ре-бер и других геометрических элементов. Поэтому для построения диаграмм состояния пятиком-лонентных взаимных систем из трех катионов и трех анионов требуется особая четырехмерная фигура - призматический гексаэдроид. [7]
Поэтому пентатоп, например, недостаточно пригоден для изображения рассматриваемой системы ввиду того, что его пять вершин геометрически равноценны. [8]
Ни пентатоп, ни тетраэдрический гексаэдроид не имеют такого числа вершии, ребер и других геометрических элементов. Поэтому для построения диаграмм состояния пятиком-понентных взаимных систем из трех катионов и трех анионов требуется особая четырехмерная фигура - призматический гексаэдроид. [9]
Поэтому пентатоп, например, недостаточно пригоден для изображения рассматриваемой системы ввиду того, что его пять вершин геометрически равноценны. [10]
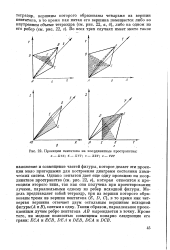 |
Проекции пентатопа на координатные пространства. a - XYZ. б - XYT. e - XZT. г - YZT. [11] |
Однако пентатоп дает еще одну проекцию на координатное пространство ( см. рис. 22, в), которая относится к проекциям второго типа, так как она получена при проектировании лучами, параллельными одному из ребер исходной фигуры. Модель представляет собой тетраэдр, три из вершин которого образованы тремя из вершин пентатопа ( Е, D, С), в то время как четвертая вершина отвечает двум остальным вершинам исходной фигуры ( А и Б), слитым в одну. Таким образом, параллельное проекционным лучам ребро пентатопа АВ вырождается в точку. [12]
Проекции пентатопа на три координатные плоскости по методу Радищева. [13]
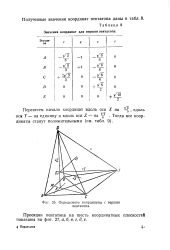 |
Значения координат для вершин пентатопа. [14] |
Проекции пентатопа на шесть координатных плоскостей показаны на фиг. [15]
Страницы: 1 2 3 4