Больца
Cтраница 1
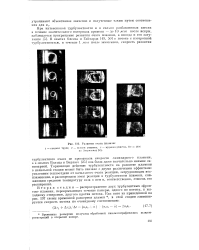 |
Развитие очага пламени. [1] |
Больца и Берлаго 125 ] она была даже значительно меньше ламинарной. Тормозящее действие турбулентности па развитие пламени в начальной стадии может быть связано с двумя различными эффектами: усилением теплоотдачи от начального очага реакции, затрудняющим воспламенение, и расширением зоны реакции в турбулентном пламени, снижающим среднюю температуру газа в нем и, соответственно, степень его расширения. [2]
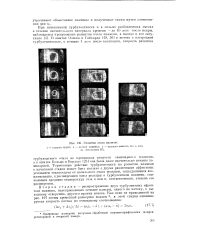 |
Развитие очага пламени. [3] |
Больца и Берлаге [25] она была даже значительно меньше ламинарной. Тормозящее действие турбулентности на развитие пламени в начальной стадии может быть связано с двумя различными эффектами: усилением теплоотдачи от начального очага реакции, затрудняющим воспламенение, и расширением зоны реакции в турбулентном пламени, снижающим среднюю температуру газа в нем и, соответственно, степень его расширения. [4]
Так как в задачах Майера и Больца известно конечное условие / () в виде (18.20), они широко применяются в различных численных методах расчета оптимального управления. [5]
Сформулированную выше задачу легко свести к задаче Майера - Больца классического вариационного исчисления. Условие стационарности в задаче Майера - Больца приводит к следующему необходимому условию. [6]
Значения предела обнаружения получены на основании данных Сендела [14], Больца [15] и Пайнта [16], приведенных к 1 см поглощающего слоя и минимальному объему пробы 1 мл. Эти данные не обязательно соответствуют условиям выполнения закона Бера. [7]
В зависимости от способа задания минимизируемого функционала различают задачи Лагранжа, Майера и Больца. [8]
Развитие теории оптимизации подчеркивает могущество и большое практическое значение классических методов вариационного исчисления, особенно методов Майера и Больца. [9]
Сразу же оговоримся, что развиваемые здесь методы для задачи Лагранжа могут применяться и для исследования задач Майера и Больца. [10]
Развитие теории оптимизации ярко подчеркивает могущество и большое практическое значение классических методов вариационного исчисления, особенно методов Майера и Больца. [11]
В более общем случае, когда рассматривается вариационная задача на условный минимум ( задача н форме Лаграшка, Майера пли Больца), формулировка Я. Дифференциальные условия связи и граничные условия в присоединенной задаче на минимум 2 - й вариации получаются в результате варьирования соответствующих условий исходной вариационной задачи. Определение сопряженной: точки остается по форме таким же. Для неотрицательности 2 - й вариации функционала на классе присоединенных экстремалей, удовлетворяющих присоединенным условиям для концов, должно выполняться Я. [12]
В классической постановке основная задача об оптимальном управлении (6.6) - (6.7) ( или ее модификации) ставится в форме известной вариационной проблемы Майера - Больца. [13]
В тех случаях, когда граничные условия и функционал заданы в более общем виде, чем в ( 3), ( 4) и ( 1) [ напр. Больца задача с подвижными концами, вариационная задача со свободными ( подвижными) концами ], к необходимым условиям оптимальности ( 6), ( 7) добавляются трансверсальности условия. [14]
Сформулированную выше задачу легко свести к задаче Майера - Больца классического вариационного исчисления. Условие стационарности в задаче Майера - Больца приводит к следующему необходимому условию. [15]
Страницы: 1 2