Большинство - реальная задача
Cтраница 2
В данной задаче синтеза, которая формулируется как задача целочисленного математического программирования, перебор осуществляется на множестве малой мощности, что допускает даже полный перебор. Но большинство реальных задач компоновочного синтеза имеет гораздо большую размерность, поэтому при их решении допустим только частичный перебор. [16]
В рассмотренной задаче структурного топологического синтеза, формулируемой как задача целочисленного математического программирования, перебор осуществляется на множестве малой мощности, что допускает даже полный перебор. Но большинство реальных задач структурного синтеза имеет гораздо большую размерность, поэтому при их решении допустим только частичный перебор. Так, количество просматриваемых вариантов L может оказаться экспоненциальной функцией размерности задачи п: L fee, где k - коэффициент пропорциональности. [17]
При этом чрезмерное увеличение а может лишь увеличить такие колебания. В большинстве реальных задач оптимальное значение множителя а подбирают путем численных экспериментов. [18]
Метод требует определения матрицы вторых производных. В большинстве реальных задач нельзя выписать в явном виде выражения для элементов матрицы G или получение их достаточно трудоемко. [19]
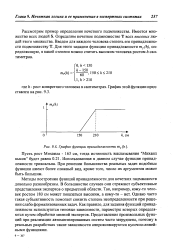 |
График функции принадлежности т ( h. [20] |
Пусть рост Михаила - 163 см, тогда истинность высказывания Михаил высок будет равна 0.21. Использованная в данном случае функция принадлежности тривиальна. При решении большинства реальных задач подобные функции имеют более сложный вид, кроме того, число их аргументов может быть большим. [21]
Необходимость такого подхода обосновывается тем, что с ростом размерности трудоемкость ( сложность) решения задач растет невероятно быстро. Беллмана, характерно для большинства реальных задач математического программирования. [22]
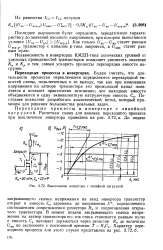 |
Выключение инвертора с линейной нагрузкой. [23] |
Последнее позволяет разработать аналитический метод, который применим для решения большинства реальных задач. [24]
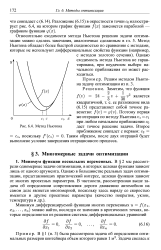 |
Метод Ньютона даст точное решение задачи. Второе. [25] |
В § 2 мы рассмотрели одномерные задачи оптимизации, в которых целевая функция зависит лишь от одного аргумента. Однако в большинстве реальных задач оптимизации, представляющих практический интерес, целевая функция зависит от многих проектных параметров. [26]
Однако при практическом использовании точных математических методов в том приложении, какое им дано в указанных выше работах, встречаются известные трудности. Во-первых, в имеющихся математических моделях задачи построения производственной программы не учитывается ряд важных планово-организационных требований таких, например, как необходимость непрерывного и равномерного производства одного изделия в смежных месяцах, необходимость концентрации производства конструктивно-однородных изделий и др. Во-вторых, алгоритмы и методы, полнее учитывающие реальные производственные условия, требуют значительного увеличения системы ограничений задачи. При этом для большинства реальных задач разрешаемая матрица имеет столь значительную размерность, операция с которой требует применения весьма мощных ЭВМ. [27]
На первый взгляд эти требования могут показаться достаточно слабыми. Действительно, среди людей, которые не сталкивались близко с решением задач, довольно широко распространено мнение, что большинство проблем удовлетворяет этим требованиям, В конце концов для многих задач эти факты кажутся очевидными, и нет никакой необходимости рассматривать много решений. Однако при более близком изучении большинство реальных задач не удовлетворяет этим требованиям, включая приведенные в разд. [28]
Робинсон разработал метод резолюций, который позволяет автоматически доказывать теоремы при наличии набора исходных аксиом. На основе метода резолюций француз Альбер Кольмероэ в 1973 г. создает язык логического программирования Пролог. Однако большинство реальных задач не сводится к набору аксиом, и человек, решая производственные задачи, не использует классическую логику, поэтому логические модели при всех своих преимуществах имеют существенные ограничения по классам решаемых задач. [29]
Функциональный анализ не всегда завершается полным строгим решением, так как основным назначением может быть разработка базовой математической модели функционирования. Разработка базовой модели позволяет более глубоко вникнуть в задачу, более полно понять физические законы и принимаемые допущения. Она особенно предпочтительна при решении новых задач, при этом во многих случаях удовлетворяются приближенной оценкой значения величин, существенных для задачи, и не ищут путей точного их определения. Иногда найти такие пути очень трудно или вовсе невозможно. Сопоставление приближенных значений величин различных параметров в базовой модели нередко создает основу для построения правильной картины развития процесса, для выделения в ней основного и отбрасывания второстепенных частностей. Большинство реальных задач функционального анализа при построении базовой математической модели функционирования лучше всего решать, используя обобщенный подход, и особенно, когда формальный подход совсем неприемлем. В обобщенном подходе из-за наличия нескольких функциональных свойств используют метод теории подобия и метод размерностей. [30]
Страницы: 1 2 3