Периодичность - потенциал
Cтраница 1
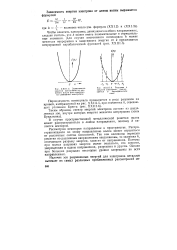 |
Зависимость энергии электронов от волнового числа для совершенно свободных электронов. [1] |
Периодичность потенциала проявляется в ряде разрывов на кривой, изображенной на рис. XXIII. [2]
Периодичность потенциала проявляется в ряде разрывов на кривой, изображенной на рис. XXIV. [3]
Периодичность потенциала означает и периодичность, или, как говорят, трансляционную инвариантность самого гамильтониана. [4]
 |
Периодичность потенциалов ионизации. [5] |
Периодичность потенциалов также находится в тесной связи с периодичностью свойств. [6]
Периодичность потенциалов ионизации также находится в тесной связи с периодичностью свойств. [7]
Учет периодичности потенциала, действующего на электроны в идеальном кристалле, позволяет установить, что их энергетический спектр имеет структуру квазинепрерывных полос или зон, разделенных участками запрещенных значений энергии, а волновая функция представляет плоскую волну, промодулированную в такт кристаллической решетке. Каждой энергетической зоне отвечает определенная область возможных значений вектора k в обратной решетке - зона Брил-люэна. Все эти результаты вытекают только из трансляционной инвариантности кристалла. Учет точечной симметрии решетки позволяет также получить ряд общих сведений об электронном энергетическом спектре. [8]
 |
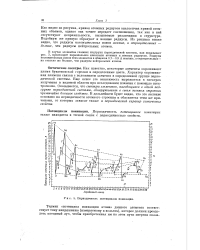
Туннельное прохождение электронов через р-п-пере. ход. [9] |
Нарушение периодичности потенциала, вызванное дефектами решетки ( примесными атомами, вакансиями и др.), приводит к возникновению в запрещенной зоне дискретных уровней. [10]
Учет периодичности потенциала, действующего на электроны в идеальном кристалле, позволяет установить, что их энергетический спектр имеет структуру квазинепрерывных полос или зон, разделенных участками запрещенных значений энергии, а волновая функция представляет плоскую волну, промодулированную в такт кристаллической решетке. Каждой энергетической зоне отвечает определенная область возможных значений вектора k в обратной решетке - зона Брил-люэна. Все эти результаты вытекают только из трансляционной инвариантности кристалла. Учет точечной симметрии решетки позволяет также получить ряд общих сведений об электронном энергетическом спектре. [11]
Тепловые колебания решетки нарушают периодичность потенциала, действующего па электрон. [12]
Граница кристалла является естественным нарушением периодичности потенциала кристаллической решетки. [13]
Важный вывод заключается в том, что предположение о периодичности потенциала приводит к появлению энергетической щели, которой нет в модели свободных электронов. [14]
Наиболее характерным из условий, в которых находятся электроны в кристалле, является периодичность потенциала, отражающая особенности структуры кристаллической решетки. Учета периодичности потенциала достаточно для того, чтобы качестве н-н о описать поведение электронов в кристалле, тогда как точное решение задачи из-за огромного числа частиц вообще теряет смысл. Например, характерные черты радиоактивного ос-распада ядра можно описать с помощью модели простого потенциального барьера, хотя точный потенциал а-частицы в ядре не известен. [15]
Страницы: 1 2